中学受験の合否は算数によって決まると言っても過言ではないほど、算数は重要な科目です。
難関校の入試では、大人も頭を悩ませるような問題が出題され、それを制限時間内に解かなければなりません。
また、中学受験の算数の難易度は、昔よりも難しくなっており、中学受験塾はその難易度に対応できるようにテキストや授業内容を改定していますので、受験生はより素早く正確に問題を解けるよう、様々なコツを学んでいく必要があります。
今回は、中学受験の算数で覚えておきたいとても重要なポイントを13個ご紹介します。
もちろん、暗記していなくても導くことができるものが大半ですが、難関校を受験する受験生の多くが血肉にしているポイントですので、覚えておかないと、素早さや正確さで負けてしまう可能性があります。受験生はぜひしっかり理解し、覚えるようにしましょう。
分数と小数の変換
頻繁に登場し、分数と小数を素早く変換できる必要のあるものがいくつかあります。
以下の分数と小数はすべて暗記しましょう。
| 分数 | 小数 |
|---|---|
| 1/2 | 0.5 |
| 1/4 | 0.25 |
| 3/4 | 0.75 |
| 1/5 | 0.2 |
| 2/5 | 0.4 |
| 3/5 | 0.6 |
| 4/5 | 0.8 |
| 1/8 | 0.125 |
| 3/8 | 0.375 |
| 5/8 | 0.625 |
| 7/8 | 0.875 |
頻出かけ算
先程ご紹介した分数と小数の変換でも出てきた数字が出てきます。
以下の頻出のかけ算は暗記しておくと便利です。
- ２５×４＝１００
- １２５×８＝１０００
- １２×１５＝１８０
この３つに関連して、計算の工夫を身に着けておきましょう。
かけ算において、一方の数の1の位が5（1の位が0のときは10の位）、もう一方の数が偶数の場合、１の位が5の数を2倍し、もう一方の数を2で割りましょう。
そうすると、筆算を使わずに計算できることが多くありますので、計算ミスを減らすことができます。
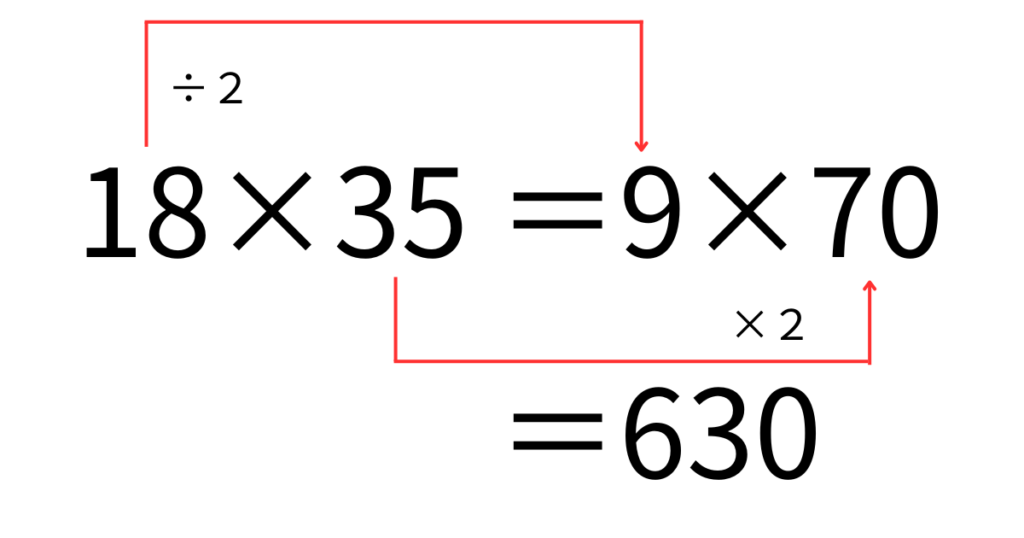
平方数
平方数とは、同じ整数同士をかけてできる数のことです。
以下の９つはすべて暗記しましょう。
- １１×１１＝１２１
- １２×１２＝１４４
- １３×１３＝１６９
- １４×１４＝１９６
- １５×１５＝２２５
- １６×１６＝２５６
- １７×１７＝２８９
- １８×１８＝３２４
- １９×１９＝３６１
暗記する理由ですが、単純にかけ算を素早く解くためだけではありません。
最も大きな理由は、規則性の問題などにおいて、かけ算の結果（１４４や２８９など）だけがあらわれ、これが平方数であることを見抜くことが求められるからです。
つまり、平方数をみたら、それが平方数であることに気づき、なにを掛け合わせた数であるかを思い出す必要があります。
立方数
立方数とは、同じ整数を３回かけあわせてできる数のことです。
以下の８つを暗記しましょう。
- ２×２×２＝８
- ３×３×３＝２７
- ４×４×４＝６４
- ５×５×５＝１２５
- ６×６×６＝２１６
- ７×７×７＝３４３
- ８×８×８＝５１２
- ９×９×９＝７２９
平方数と比べれば覚える優先順位は下がりますので、もしかけ算する必要がある時は、曖昧な記憶を頼りにして間違えるよりは、その場でしっかり計算したほうがよいでしょう。
ただし、平方数と同様、規則性の問題などにおいて、立方数であることに気づくことが求められる問題が時々ありますので、気づけるようになっておくことが大切です。
3.14の計算
円周率の計算は、以下の８つを必ず暗記しましょう。
- ３.１４×２＝６.２８
- ３.１４×３＝９.４２
- ３.１４×４＝１２.５６
- ３.１４×５＝１５.７
- ３.１４×６＝１８.８４
- ３.１４×７＝２１.９８
- ３.１４×８＝２５.１２
- ３.１４×９＝２８.２６
この８つさえ覚えておけば、もう少しかけ算が大きくなっても、あとは計算の工夫で簡単に計算することができます。
おうぎ形の角度と約分した分数
おうぎ形の問題では、円周の長さや面積を求める際に、その中心角に応じてかけ算をする必要があります。
微妙な角度の場合は丁寧にその場で約分したほうが良いですが、頻出な角度がありますので、それらは約分した後の分数を覚えておくと素早く正確に計算することができます。
正直、約分したとしてもそこまで時間がかかりませんので、これらを必死で覚える必要はありません。
問題をこなしていく中で、自然と暗記してしまうことが理想です。
- ３０°／３６０＝１／１２
- ４５°／３６０＝１／８
- ６０°／３６０＝１／６
- ９０°／３６０＝１／４
- １２０°／３６０＝１／３
- １８０°／３６０＝１／２
素数
素数をテーマにした問題は頻出です。
以下に記載した整数が素数であることはすぐに判別できるよう、覚えておきましょう。
２ ３ ５ ７ １１ １３ １７ １９ ２３ ２９ ３１ ３７ ４１ ４３ ４７ ５３ ５９ ６１ ６７ ７１ ７３ ７９ ８３ ８９ ９７
ただし、これらの数字を暗唱できるほどに丸暗記する優先度は高くありません。
もし覚える場合も、赤字のあたりまでで大丈夫です。
あくまで、素数であることを判別できることが大切ですので、５７、８７、というような数字に出会った時に、素数ではないと判別できることも重要です。
問題を解いていく中で様々な倍数や素数に触れ、自然と素数なのか、そうではないのかを的確に判断できるようになっていくことが理想です。
倍数の見分け方
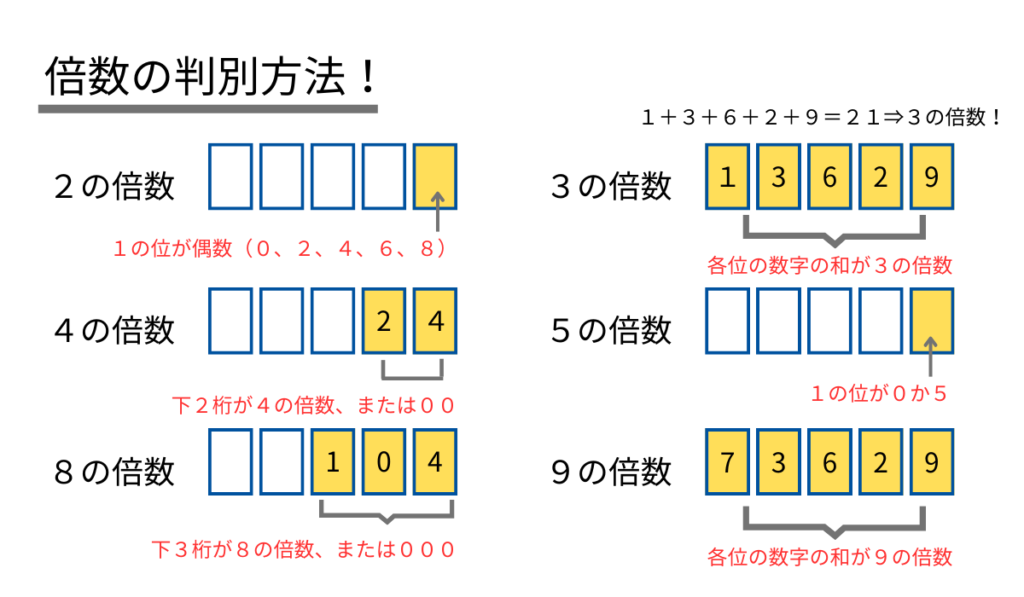
以下の倍数のルールは必ず暗記しましょう。
- ２の倍数⇒１の位が０、２，４，６，８
- ３の倍数⇒各位の数字の和が３の倍数
- ４の倍数⇒下２桁が４の倍数、または００
- ５の倍数⇒１の位が０、５
- ８の倍数⇒下３桁が８の倍数、または０００
- ９の倍数⇒各位の数字の和が９の倍数
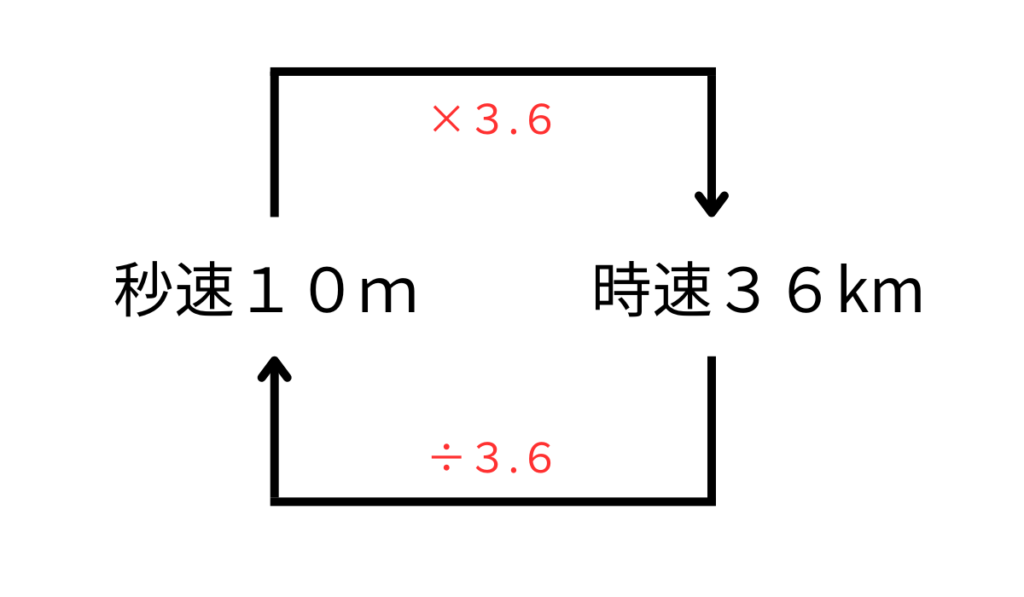
秒速と時速の変換
ｍ（メートル）で表された秒速を３.６倍すると、km（キロメートル）の時速に変換することができます。逆にいうと、km（キロメートル）の時速を３.６で割ると、ｍ（メートル）の秒速にすることができます。
なぜ３.６倍の関係になっているかを以下でご説明します。
例えば、秒速１０ｍで考えます。
秒速１０ｍとは、１秒間に１０ｍ進む速さのことですから、１分間（60秒）では、
１０×６０＝６００ｍ
進むことになり、つまり、分速６００ｍとなります。
さらに、1時間（60分）では、
６００×６０＝３６０００ｍ
進むことになります。
３６０００ｍは１０００で割るとkmに変換でき、３６kmですから、時速３６kmになります。
ここで、秒速と時速の関係を見てみると、
１０×３.６＝３６
となり、３.６倍の関係になっていることが分かります。
秒速を分速にするために60倍、分速を時速にするためにさらに60倍、そして単位をmからkmに変換するために１０００で割っていますので、
６０×６０÷１０００＝３.６倍
になっているのです。
知っておきたい素因数分解
素因数分解が求められる問題も頻出です。
数が小さければ、なんとなくなんの倍数かあたりがつくと思いますが、数が大きくなると、
「これはなにで割れるんだ・・・？素数か・・・？」
と思ってしまうこともあると思います。
そういった間違い、見逃しがないよう、以下は知っておくと役に立ちます。
ただし、もし覚えていなかったとしても「２、３、４、５、８、９の倍数のルール」「平方数」「立方数」でしっかり判別することができれば、素因数分解に気づくことができますので、覚えておくと便利というレベルで認識しておきましょう。
そのため、以下では2の倍数、５の倍数は除いてご紹介しています。
１３の倍数
９１＝１３×７
１１７＝１３×９
１７の倍数
５１＝１７×３
１１９＝１７×７
１９の倍数
５７＝１９×３
１３３＝１９×７
２３の倍数
６９＝２３×３
１６１＝２３×７
２９の倍数
８７＝２９×３
２０３＝２９×７
３７の倍数
１１１＝３７×３
２５９＝３７×７
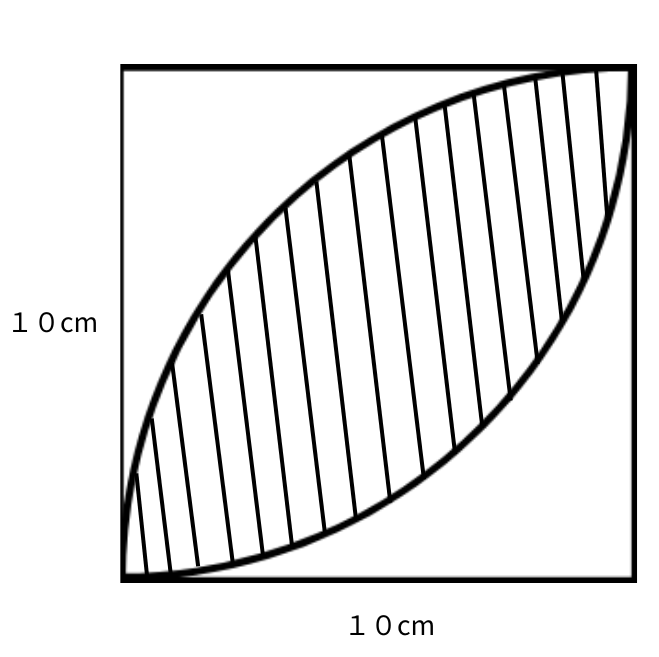
葉型の面積の求め方
以下の、斜線部分の葉型のような形に見覚えのある方は多いのではないでしょうか。
この形の面積を求める問題はかなり頻出です。
さらに難しい問題では、この形の面積を求められることを前提として、さらに発展的に考える必要があります。
実はこの形は正方形の面積に０.５７をかけることで簡単に求めることができます。
１辺が１０cmの正方形ですので、斜線部分の葉型の面積は
１０×１０×０.５７＝５７㎠
となります。
難関校では、地道に計算してしまうと非常に計算が煩雑になってしまう問題が良く出題されるため、この求め方は暗記しておきましょう。
葉型の面積は正方形の面積に０.５７をかけて求めることができる
多角形の内角の和
三角形の内角の和は１８０°、四角形の内角の和は３６０°と、これはみなさん覚えていると思います。
五角形、六角形、七角形、そしてそれ以上の多角形の内角の和はいくつになるでしょうか？
これは求める公式・ルールがありますので、仕組みをしっかり理解し、求め方を覚えておきましょう。
まず、求め方ですが、以下の式で求めることができます。
N角形の内角の和は
（Nー２）×180
で求められます。
仕組みをしっかり理解しておきましょう。
以下のように、多角形は三角形に分割することができます。
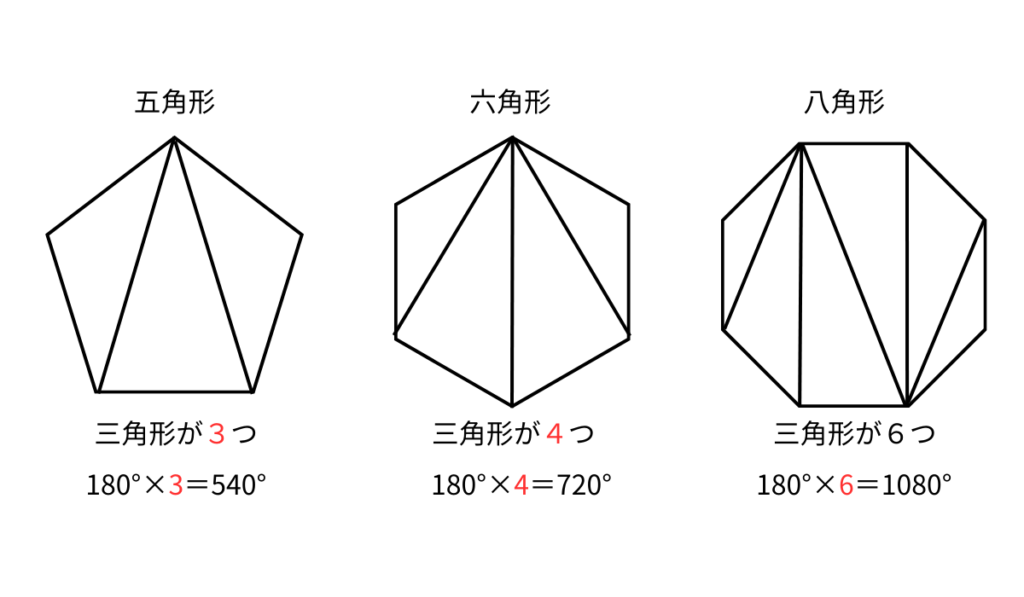
そうすると、三角形の内角の和は180°ですから、それを何倍かすれば多角形の内角に和となります。
何倍するかというと、以下の規則を見れば、N角形のNから２を引いた数の三角形に分割できるという規則性があることがわかりますので、Nー２をかければよいですね。
多角形の外角の和
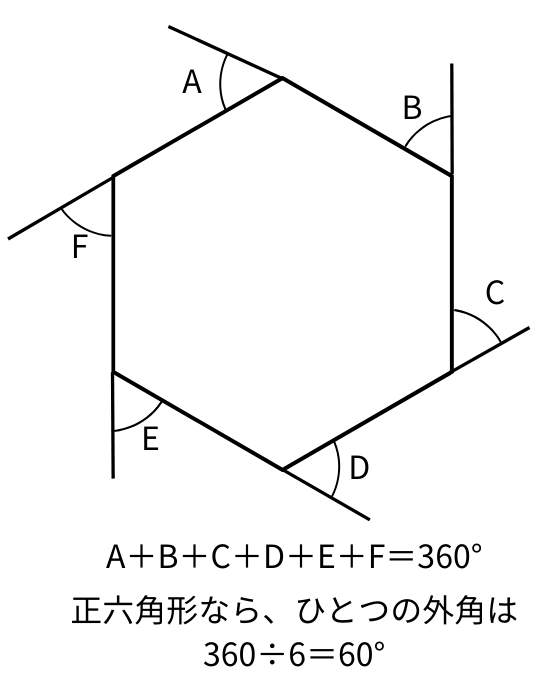
多角形の外角の和は、360°になります。
中学受験では、特に正多角形においてこれを使うことを求められます。
以下のように正多角形の１つの外角を求めることができます。
- 正三角形：３６０°÷３＝１２０°
- 正方形：３６０°÷４＝９０°
- 正五角形：３６０°÷５＝７２°
- 正六角形：３６０°÷６＝６０°
- 正八角形：３６０°÷８＝４５°
- 正十角形：３６０°÷１０＝３６°
１つの外角がわかれば、180°から外角を引けば、内角を求めることができます。
まとめ
序盤にご紹介した分数と小数の変換、円周率の計算、平方数などは、もし難関校を目指すのであればすべて覚えておくことが理想です。
計算以外のルールについては、すべてを完璧に覚えておく必要はありません。
もし忘れてしまっても、仕組みや理由を理解していれば、かならず導くことができるものばかりです。
これらを丸暗記するような勉強の仕方ではなく、これらに関連する問題に出会った時に、そういえば覚えておくと便利だったはず…と思えることで、徐々に覚えていくことが自然です。
算数は、良い意味で楽をできるような解き方方を目指すような意識が重要です。
ぜひ受験生の皆さんもこれらを参考に、日々の算数の勉強に楽しみながら取り組んでいただければ幸いです。
LEFYでは、受験生にはこういった少し知識のようなポイントをしっかり確認し、受験に向けた対策を行っています。
また、講師は難関中高一貫校出身者、プロ講師ばかりですので、問題を解いていく中でも、こういったポイントを抑えながら指導しています。
以下の記事では算数の成績のオススメ市販問題集をご紹介しています。
【中学受験算数】オススメ問題集一覧＆推奨勉強法を塾講師がご紹介！
▲レフィーのインスタグラムはこちらから
中学受験・中高一貫校生の成績UPのコツやレフィーのことについて発信しています！
LEFY公式ラインでは、中学受験と中高一貫校生の勉強に関する情報を配信しています。
LEFYマガジンの記事を定期的に通知していますので、ぜひご登録ください！
