「場合の数」はかなり多くの受験生が苦戦する単元です。
今回ご紹介する「場合の数」、そして「規則性」や「条件整理・推理」では、入試レベルでは大人でも解けないような問題が出題されます。
どんなに算数が得意な受験生でも、これらの単元は比較的苦手としていることが多いです。
今回は、小4、小5、小6の「場合の数」が苦手な受験生を対象として、「場合の数」の基本を理解し、中程度~応用のレベルの問題を解けるようになるために意識して欲しいことをご紹介します。

「場合の数」に強くなるためのポイント
その1:すべて書き出してみる!
「場合の数」が苦手なのであれば、すべて書き出してみる経験が必要です。
特に小4、小5の時期であれば、まだ時間に余裕がありますので、すべて書き出す経験をしたほうがよいでしょう。

「場合の数」では、並べ方や選び方の計算方法を学習しますが、その計算がなにを意味しているのかを理解せずに計算している受験生が大半です。
その結果、かけ算しなければいけないところで、たし算をしてしまうようなミスが多発します。
すべて書き出す中で「この計算はこれを計算しているのか!」という気づきが生まれ、基本を理解できるようになります。
「こんなの調べなくても計算で求めればいいじゃん!」と思うような問題でもスラスラと確実に調べることができるか確かめてみましょう。
それができないのであれば、自分がなにを計算しているのかを完璧に理解しているわけではないということになります。
その2:計算手順を絶対に覚えないようにする!
「場合の数」に限らず絶対にやってはいけないこととして、計算手順を覚えてしまうことが挙げられます。
正確には、
「”ならべ方”というワードがあったらかけ算だよ!」
「”ぬり分け問題”はかけ算で考えらればいい!」
というように、〇〇の場合は▲▲をすればよい、といった覚え方をしてはいけません。
特に、小4、小5の序盤の段階でこのような学び方をしてしまうと、その時期に学習する問題がシンプルで簡単であるがゆえに、上記ようなルールで正解を出すことができてしまい、自分がなにを計算しているのかわからないまま学習を終えてしまうことになるからです。
その結果、月例テストや模試になると場合の数が壊滅的になってしまうことでしょう。
「場合の数」を学習し始めた段階から、すべて書き出す経験をし、それを求めるために計算しているのだと理解することが大切です。
その3:解説はじっくり読んで完璧に理解する。必要なら親がサポート
解説には、どんな計算をして答えを求めるかが書いてあります。
しかし、なぜその計算をするのかという理由はかなり簡易的になっている、もしくは省略されていることが多いです。
つまり、上でご紹介したような、なぜその計算をするのかということを理解していることを前提として、
「この計算をするってことは、これを求めているのか」
という推理力も求められます。
しかし、「場合の数」が苦手なお子さんが自力でそれを理解することはかなり難しいことです。

保護者の方が一緒に問題を考え、その計算がなにを意味しているのかをかみ砕いて伝えてあげる必要があります。
その4:根気よく調べようとする気持ちが大切
基本が理解できたら、応用問題を解いていかなければなりません。
その際、「どんな計算をするのか?」を出発点として考えてしまう受験生が大変多いです。
しかし、応用問題では、
・部分的にかけ算で求められるが、独立しているものは足し合わせる必要があるもの
・かけ算では求められないもの
など、複雑なものを丁寧に紐解いていく必要がある問題が多数存在します。
つまり、「どんな計算をするのか?」ではなく、「どんなものを調べるように求められているのか」を出発点として考えなければいけません。
このように考えれば、一旦少し書いて調べてみることになるはずです。
少し書いて調べていく中で、
「ここはならべ方だから計算しちゃおう!」
「ここはさっき調べたやつと同じだ!」
「この場合を除けばもしかして計算で求められる…?」
といったようなことに気づくことができます。
■関連記事
【中学受験算数】オススメ問題集一覧&使い方を塾講師がご紹介!
【中学受験】算数が苦手な子でも着実に伸びる勉強法を塾講師が解説
プロが解説【中学受験】算数偏差値を伸ばす勉強方法と求められる能力。
「ならべ方&和」のしっかり理解したい例題5選!
例題①:人のならび方
問題:A君、B君、C君、D君の4人が横1列に並びます。4人の並び方は何通りありますか。
場合の数をある程度勉強した受験生であれば、
一番左は誰でもいいので4通り、2番目は1番左以外の3通り、3番目は残り2人の2通り、4番目は残り1人が必然的に決まるので、
4×3×2×1=24(通り)
とさらっと求めることができるでしょう。
言葉で理解することも大切ですが、以下のようなイメージを浮かべられるようにしておくことが重要です。
ならべ方の問題では、まずは場所を確保してあげると考えやすくなります。
下の図のように、左から1番目の場所にAがいるとすると、左から2番目の場所にはB、C、Dがきます。
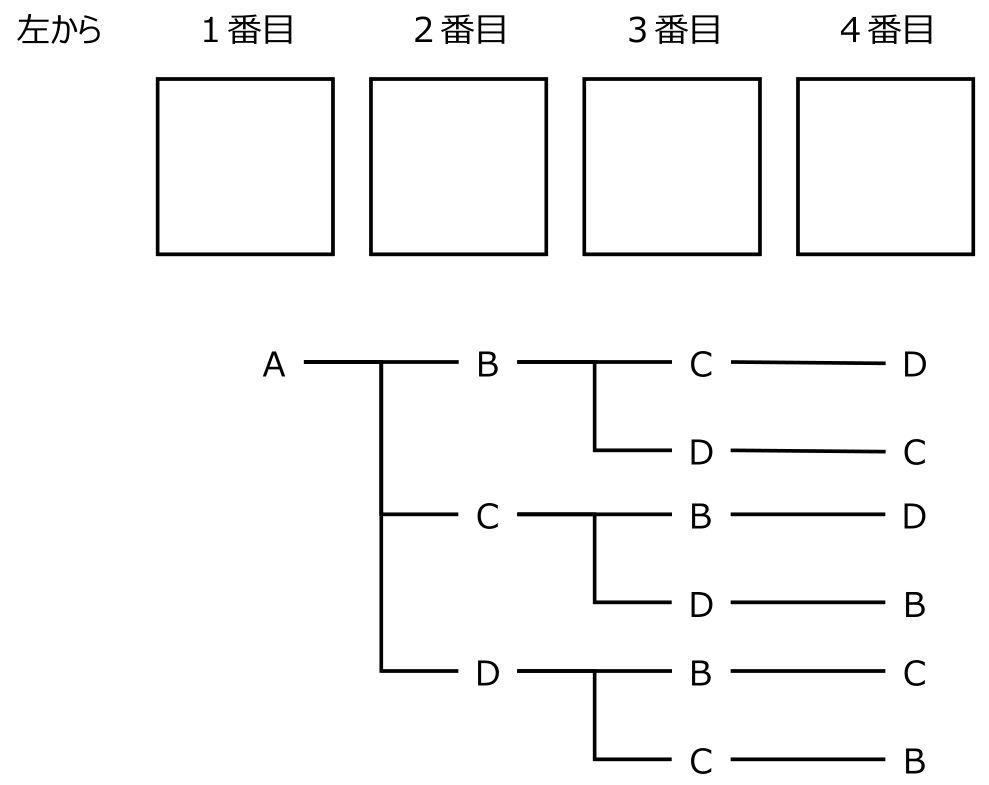
このように考えると、左から1番目の場所にAがいる場合は、6通りのならび方があります。
同様に考えると、全体では以下のようになります。
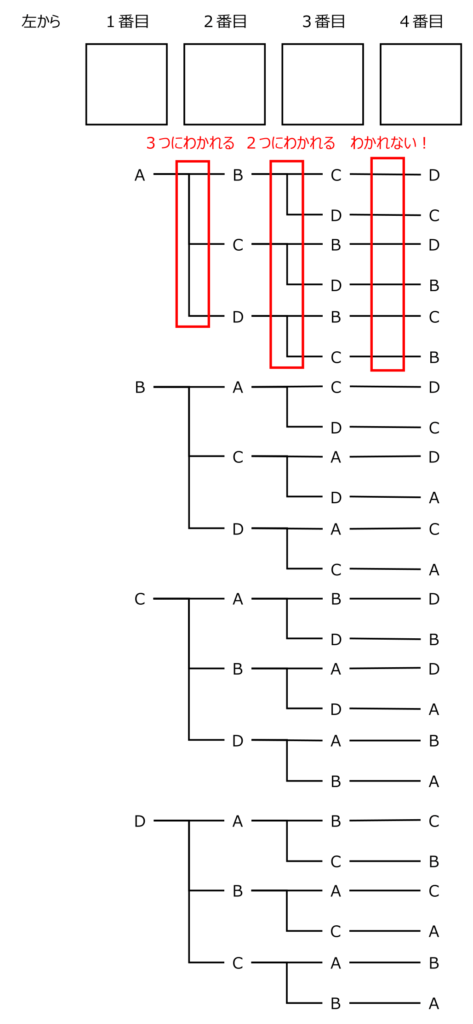
上の画像(樹形図)の一番右の列に何個文字があるかを数えるのと同じだということが分かります。
そう考えれば、一番左には4つあって、左から2番目は4つそれぞれが3つに分かれて、左から3番目はさらにそれが2つに分かれて、ということになるので、視覚的にも
4×3×2=24(通り)
という計算に納得できるはずです。
このように、自分がなにを計算しているのかをイメージできるようにしておくことが大切です。
例題②:道順(かけ算メインのもの)
問題:以下の図で、A地点からC地点まで行く最短の行き方は何通りありますか。
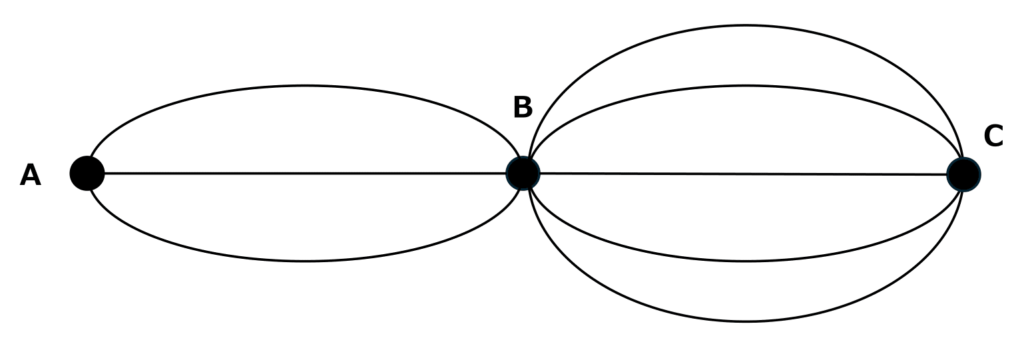
A地点からB地点までが3通り、B地点からC地点までが5通りですので、
3×5=15(通り)
です。
この問題も、上記の計算がなにを意味しているのかを理解しておくことが大切です。
まずは道に以下のように名前を付けてみます。
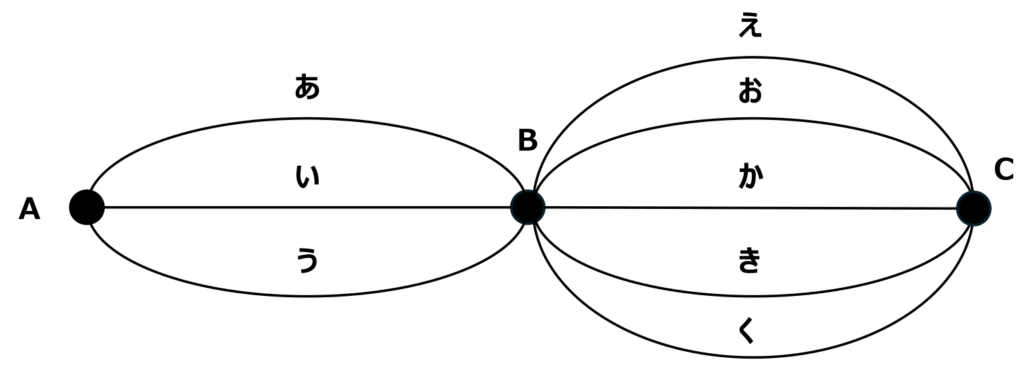
このようにすれば、A地点からB地点に行くときに通る道、B地点からC地点に行くときに通る道の組み合わせを以下のように考えることができます。
先ほどの問題と同じように、「A地点からB地点に行くときに通る道」と「B地点からC地点に行くときに通る道」の置き場所を考え、そこに何が入るのかを樹形図で考えます。
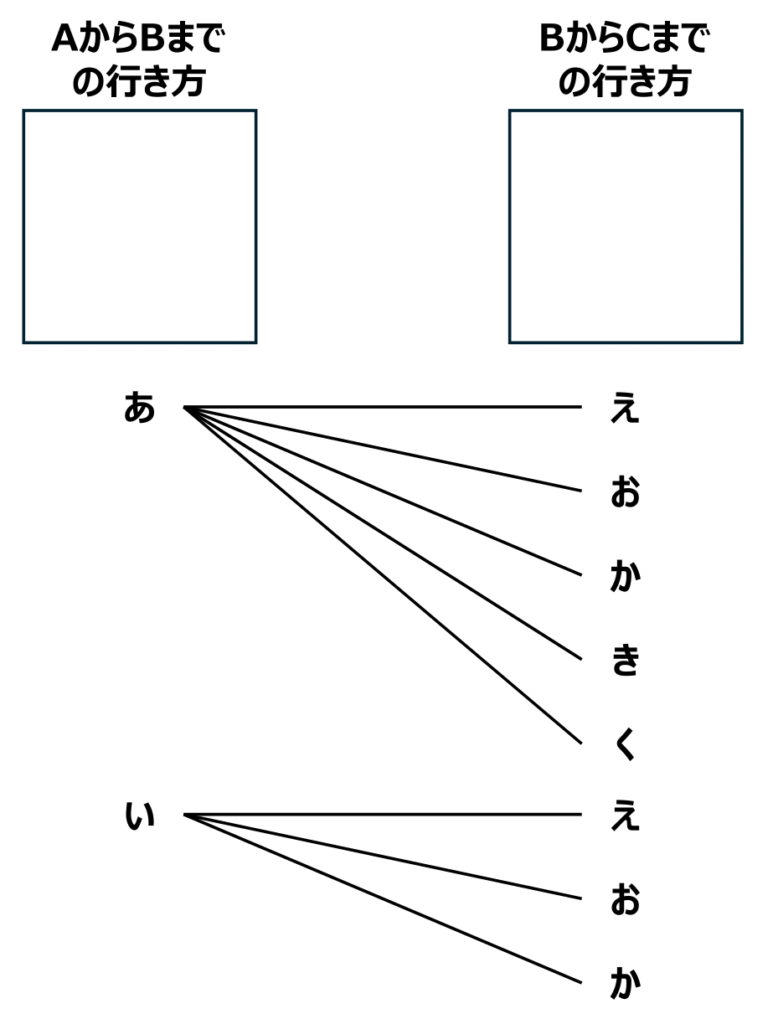
“い”以降も”あ”と同様に5通りありますから、
3×5=15(通り)
となります。
例題③:整数の作り方
問題:0、1、2、3、4、5の6枚のカードがあります。このうち3枚をならべて3ケタの整数を作ります。整数は何通り作れますか。
本問も慣れている受験生であれば、
5×5×4=100(通り)
と素早く計算できることでしょう。
これも例題①、例題②と同じように考えることができます。
まずは以下のように各位の場所を作ります。
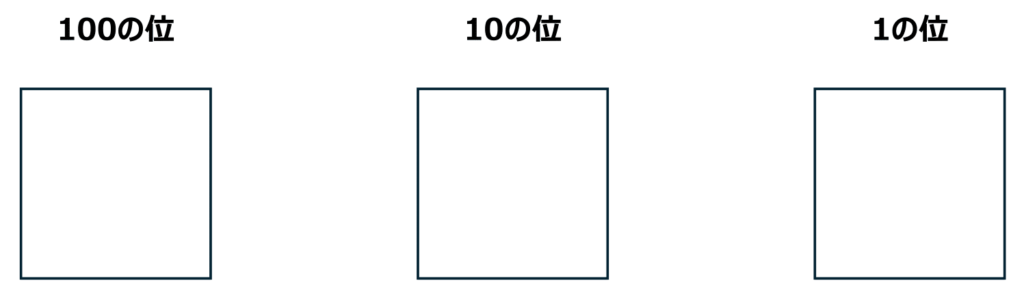
この枠に、0、1、2、3、4、5の6枚のカードのどれを置くことができるかということを考えていきます。
そうすると、以下のように樹形図で調べることができます。
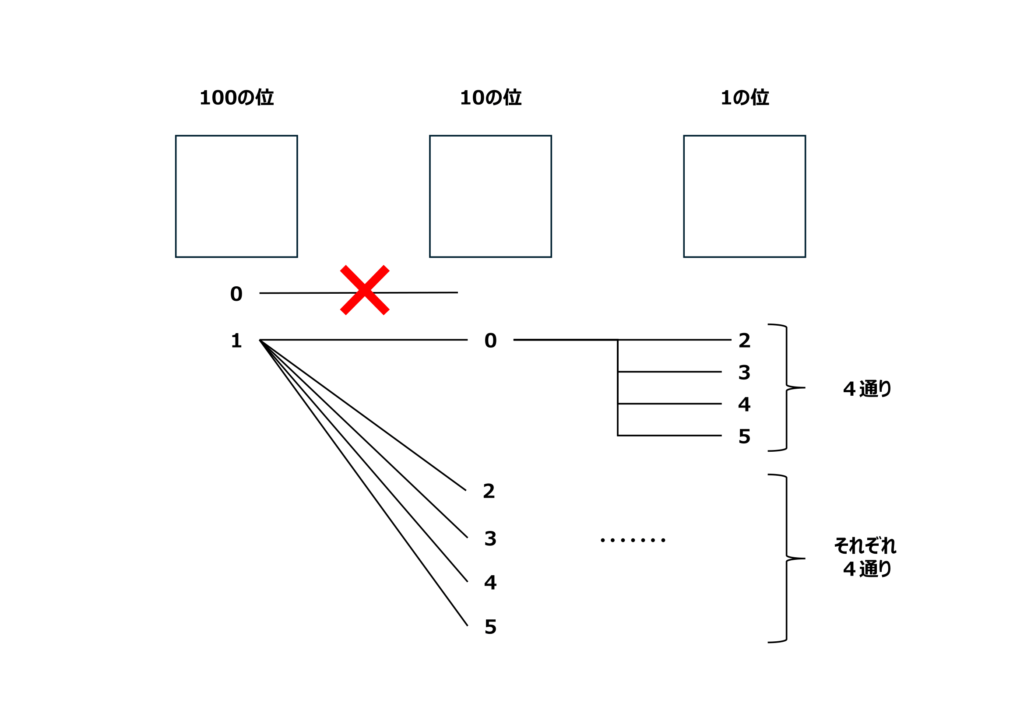
0から始まる100以上の整数は存在しないため、百の位に「0」を置くことはできない点に注意しましょう。
百の位に1、十の位に0を置くと、一の位には2,3,4,5の4通りを置くことができます。
百の位に1、十の位に2,3,4,5を置いた場合も同様に4通り置くことができると考えられます。
つまり、百の位に1を置いた時、全部で
5(十の位の個数)×4(一の位の個数)=20(通り)
が考えられます。
よって、百の位には1,2,3,4,5の5通りを置くことができるので、
5×20=100(通り)
が答えです。
最初の5×5×4=100(通り)と計算の順番は異なりますが、同じものを求めています。
例題④:ぬり分け
問題:赤、青、黄の3色を使って、下の図のA、B、C、Dの4か所をぬりわけます。となり合う部分が同じ色にならないようにするとき、何通りのぬり方がありますか。
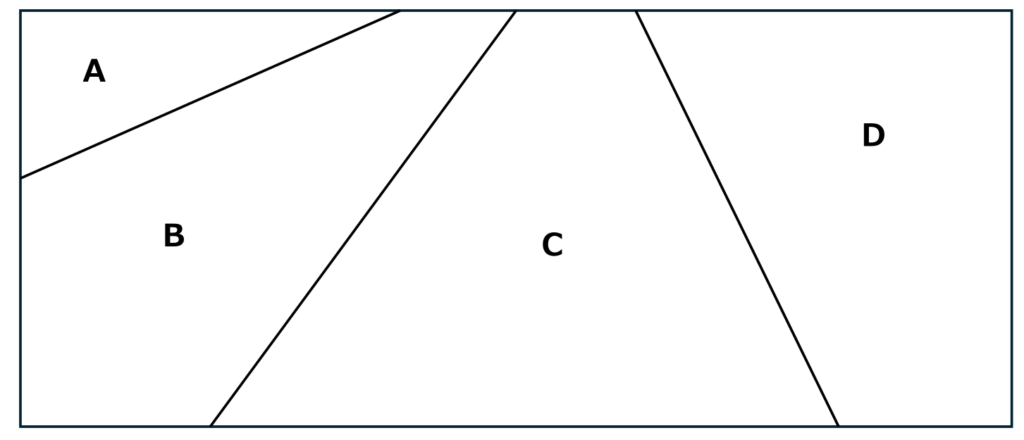
色のぬりわけ問題も、難しい問題を除けば、これまでと同じように考えることができます。
慣れていれば、Aの色は3色のどれでもよく、BはAで使った色以外の2色、CにはBで使った色以外の2色、DにもCで使った色以外の2色を使うことができるので、
3×2×2×2=24(通り)
と求めることができます。
ただし、ぬりわけの問題は、使える色の数に指定があったり、2つの箇所と隣り合うような場合がありますので、その時々の条件に応じてどのように調べ、計算するのかを適切に考えなければいけません。
そのためにも、このような初歩的なレベルの問題のうちから、以下のようなイメージを浮かべられるようにしておくことが大切です。
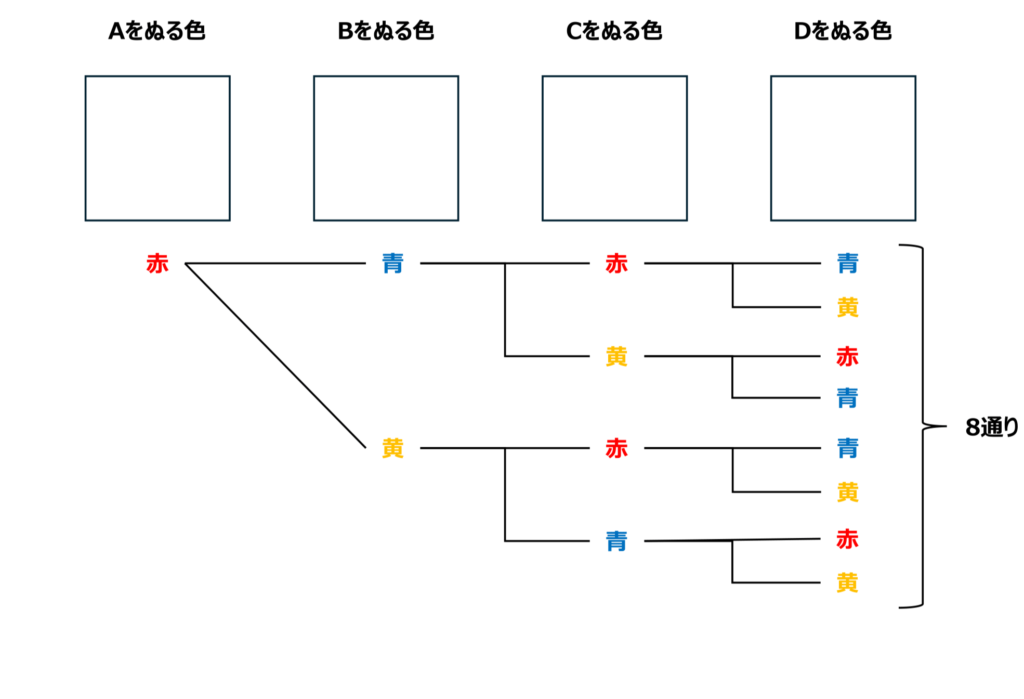
上のように樹形図を書くと、Aをぬる色を赤として考えると、ひとつ右にいくにつれて、必ず2つにわかれていくことが分かります。
つまり、Aを赤でぬる時、
2×2×2=8(通り)
で、Aは赤、青、黄の3色をぬることができますから、
8×3=24(通り)
と求めることができます。
Aをぬる色から考えていけば、
3(A)×2(B)×2(C)×2(D)=24(通り)
と計算で一発で求めることもできます。
ただし、場合の数が苦手なお子さんは、慣れていないうちは、自分が計算しているものが確かなものか検証できないことがありますので、絶対に「これはこう計算すればいい!」と覚えないようにしましょう。
例題⑤:道順(ごばんの目)
問題:下の図のような道があります。A地点からB地点まで最短で行く進み方は何通りありますか。
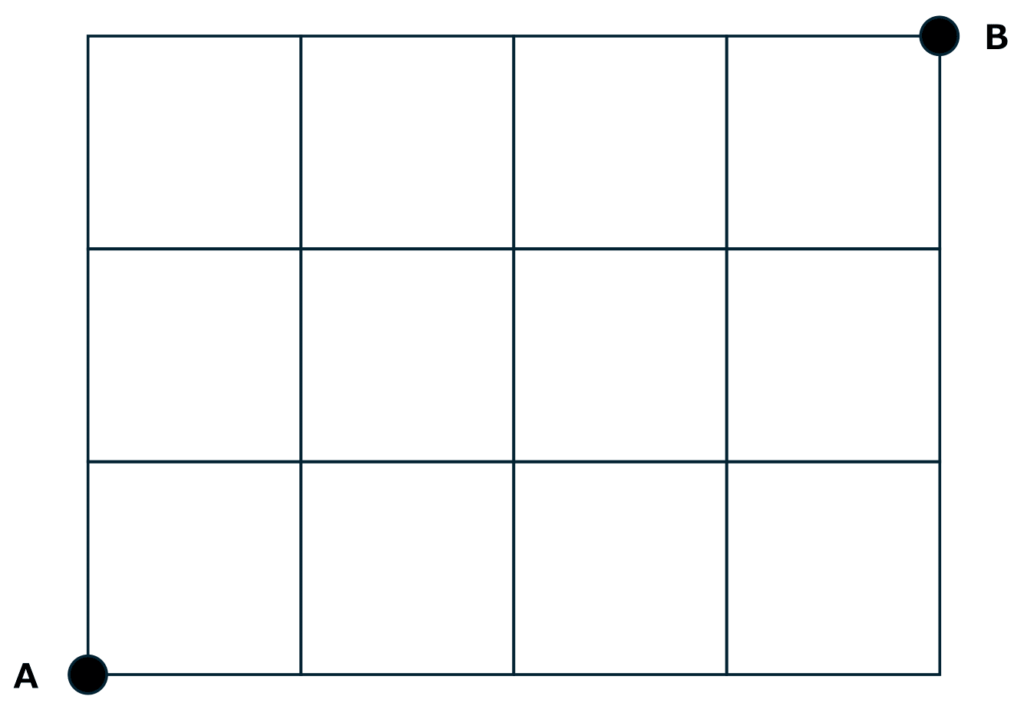
このくらいシンプルな問題であれば、多くの受験生が素早く数字を以下のように書き込み、さらっと解けるかもしれません。
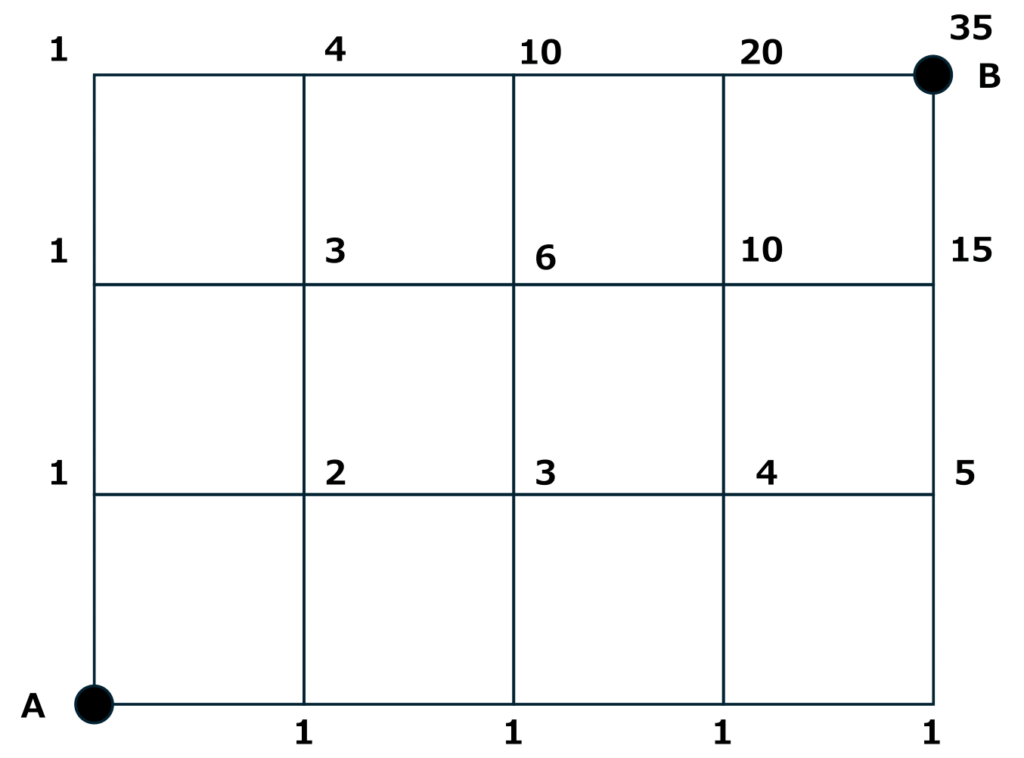
ただし、この数字がなにを意味しているのかをパッとイメージできなければ、応用問題を解けません。
以下の図のように、数字はそこにたどり着くことができる最短の道順の数を示していることを理解しておきましょう。
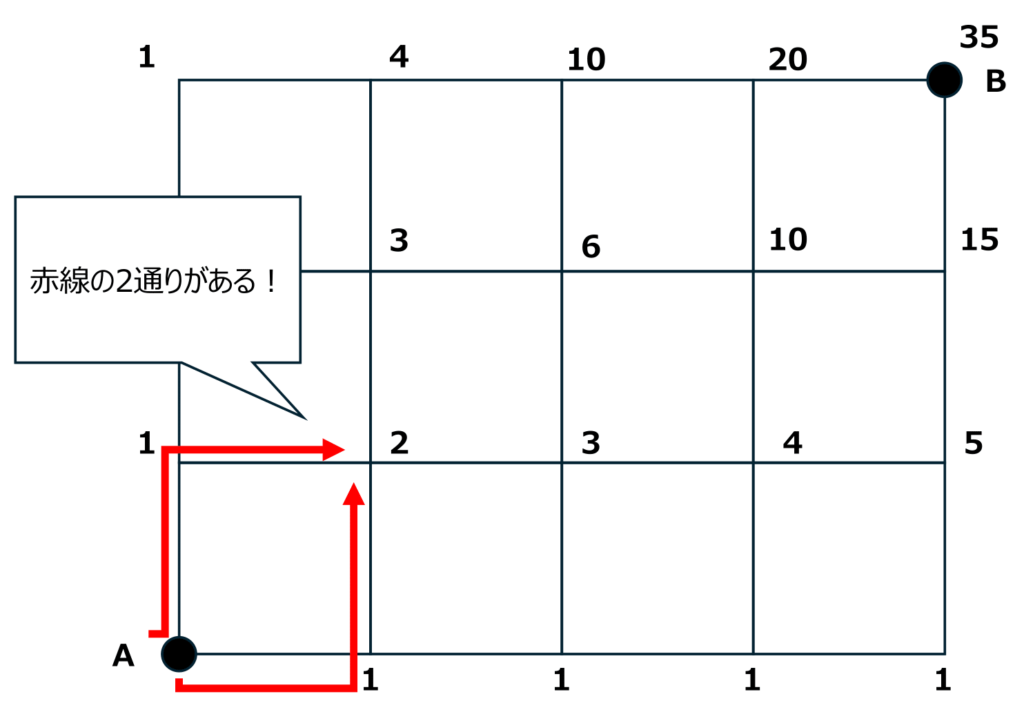
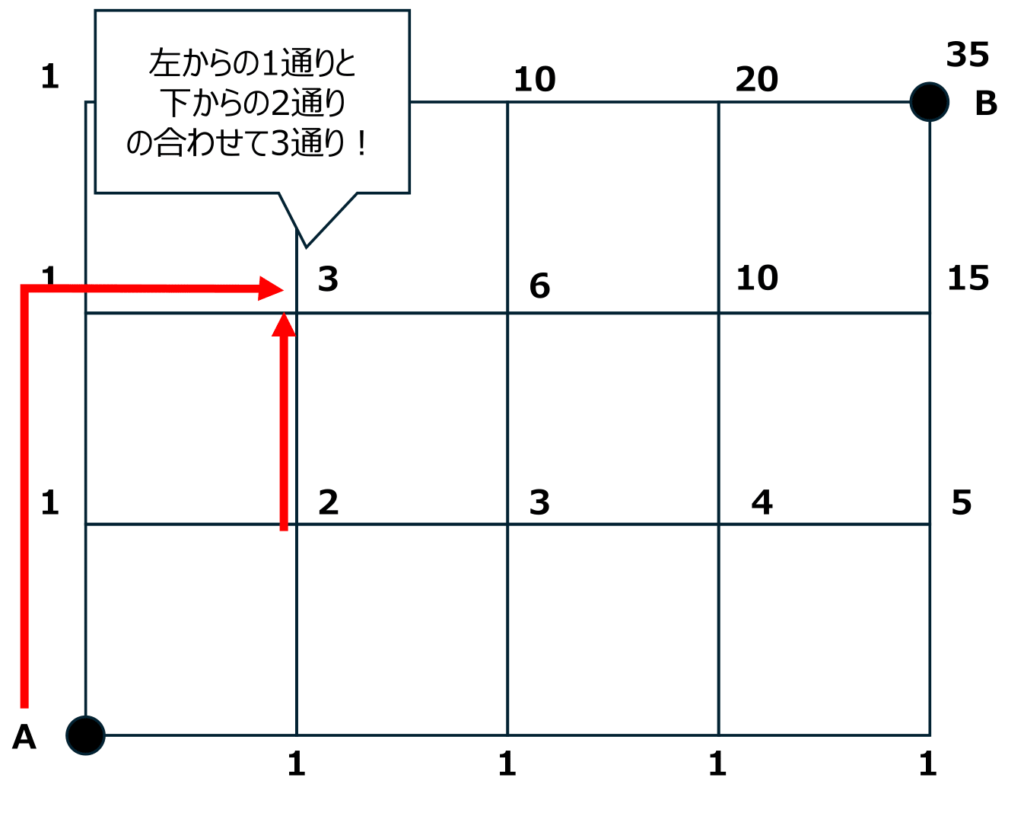
しっかりと意味を理解していれば、以下のような問題にも対応可能なはずです。
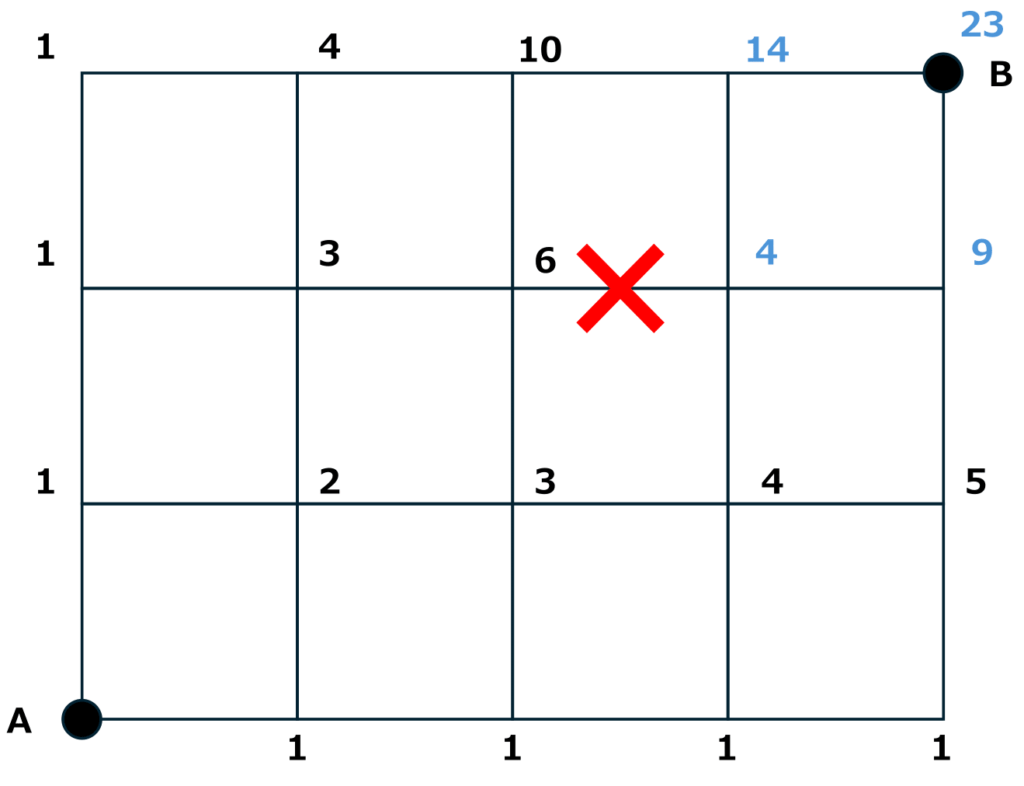
問題:下の図のような道があります。A地点からB地点まで最短で行く進み方は何通りありますか。ただし、×マークの箇所では工事中で通ることができません。
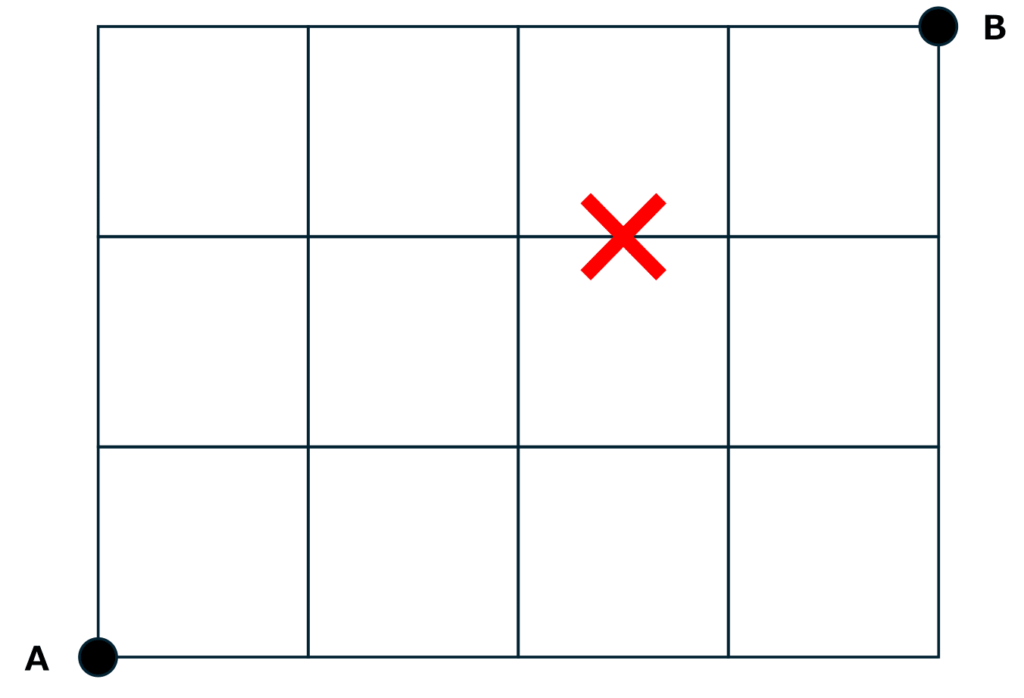
まずは工事中の×以外の箇所に数字を書き込む解き方で考えます。
青色の?マーク以外の箇所は工事中の×に関係なくたどりつくことができますので、先ほどと同様の手順で以下のように数字を書きましょう。
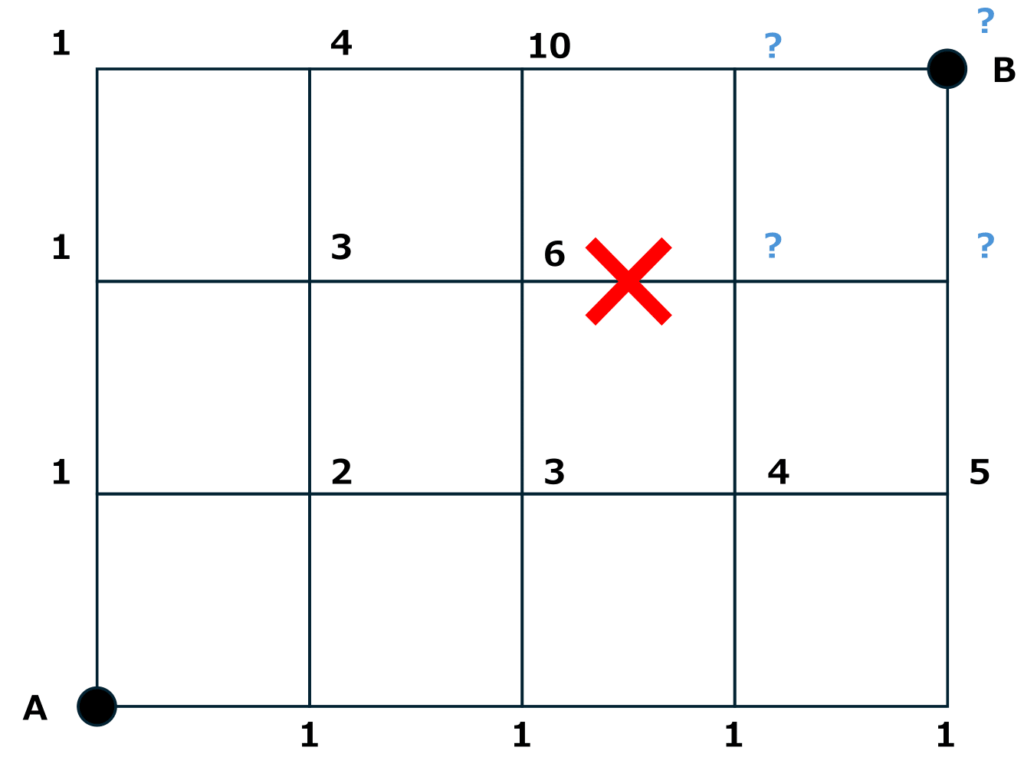
青色の?マークの箇所はどのように考えればいいのでしょうか。
シンプルに「どの地点からそこにたどりつくことができるか」を考えると、まずは以下のようにしか移動できないはずです。
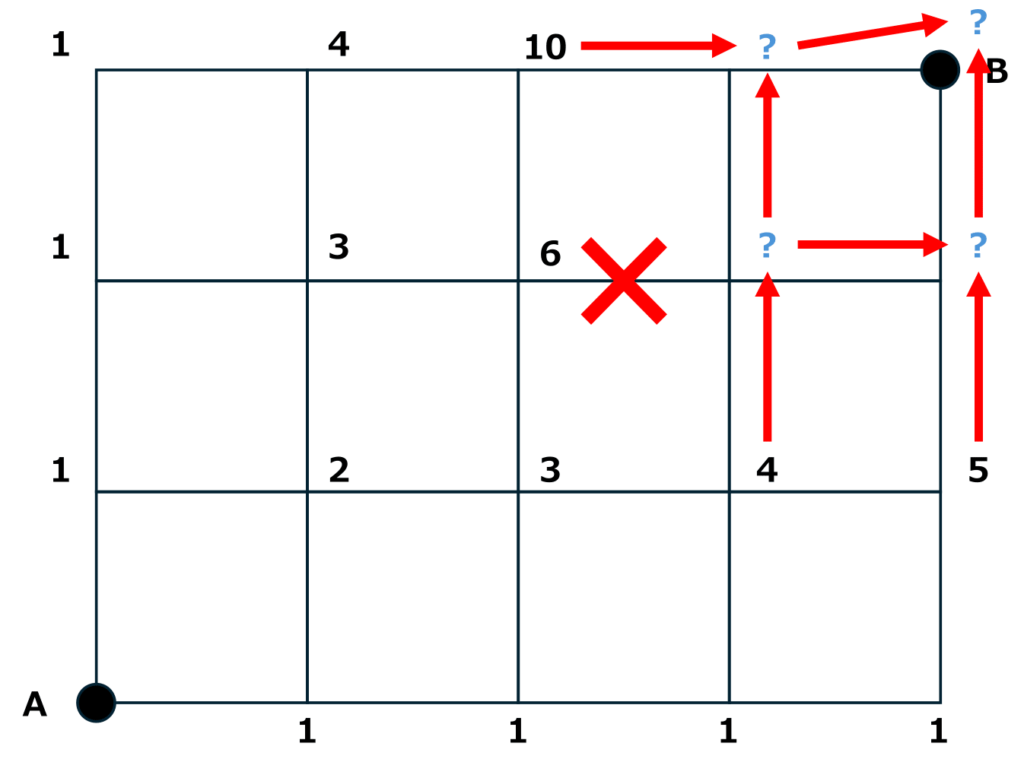
そして、以下のように答えを求めることができます。
他には「工事中の×を必ず通る行き方求め、すべての行き方から引いて求める」方法もあります。
以下のように、工事中の箇所の手前の地点までへの行き方は6通り、工事中の箇所を通った先にあるC地点からB地点までの行き方は2通りです。
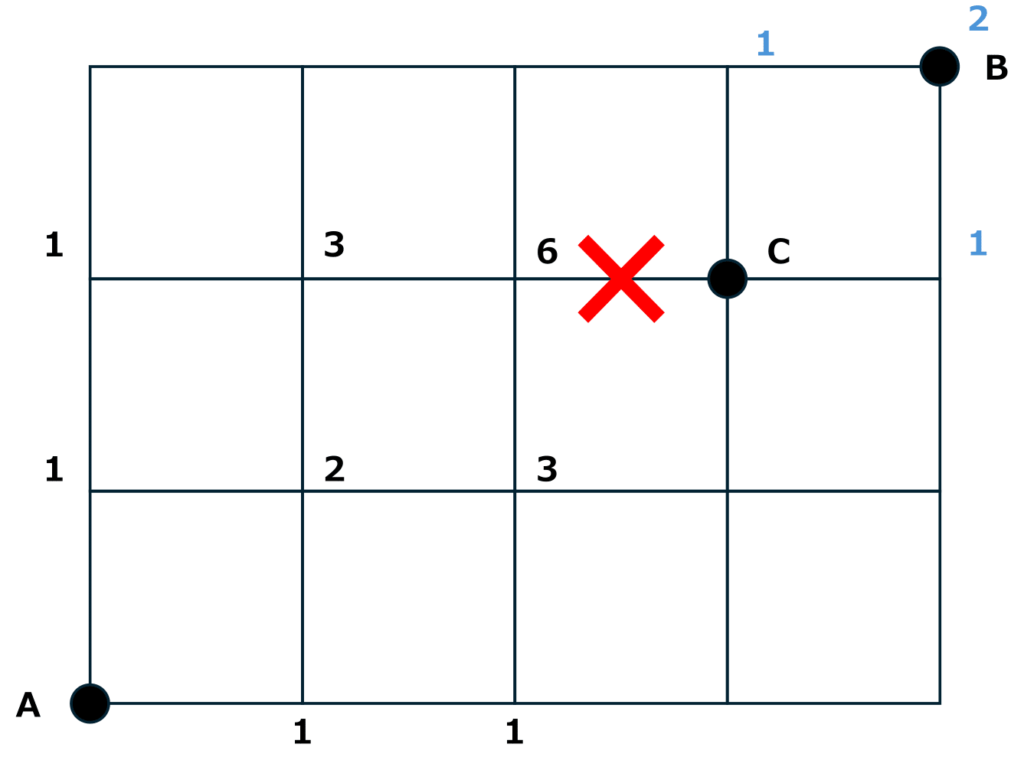
つまり、工事中の×の箇所を必ず通るA地点からB地点までの行き方は
6×2=12(通り)
※これがなぜかけ算になるのかパッとしない受験生は、例題②のように行き方に名前をつけて考えてみましょう。
すべての行き方は35通りとわかっていますから、
35ー12=23(通り)
と求めることができます。
「組み合わせ方」をしっかり理解したい例題6選!
例題①:区別された複数の中から組み合わせを選ぶ
問題:A、B、C、D、E、Fの6人の中から、委員会のメンバーを2人選びます。2人の選び方は何通りありますか。
先ほどまでの問題と異なる点は、置き場所に名前が同じで区別することができない点です。
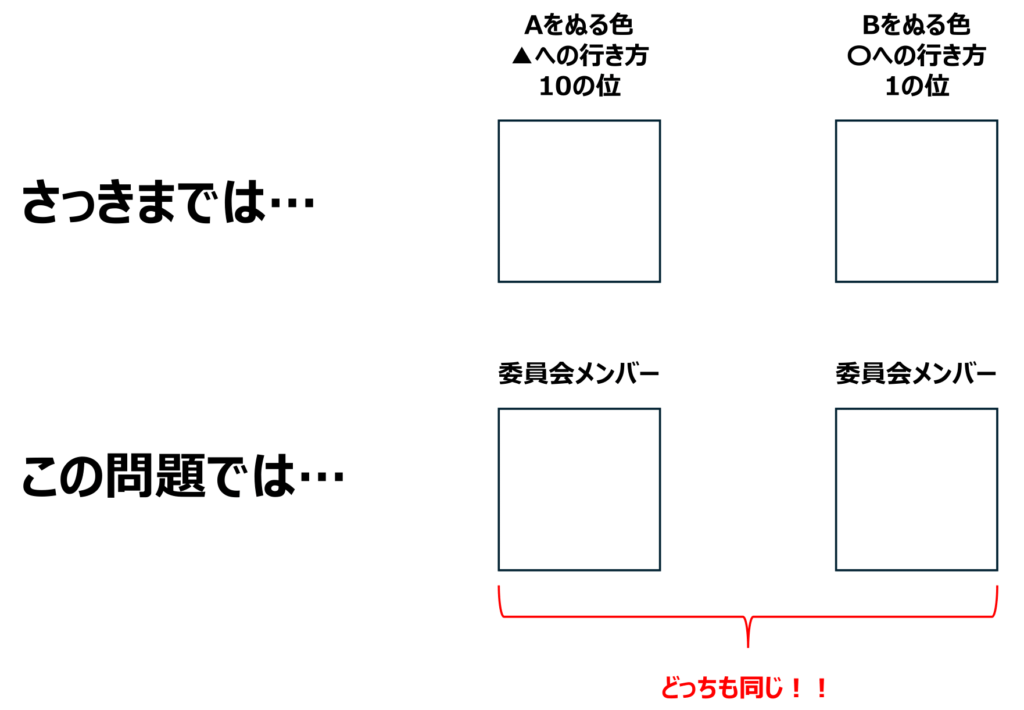
つまり、以下のようなならべ方は同じものとしてカウントされてしまいます。
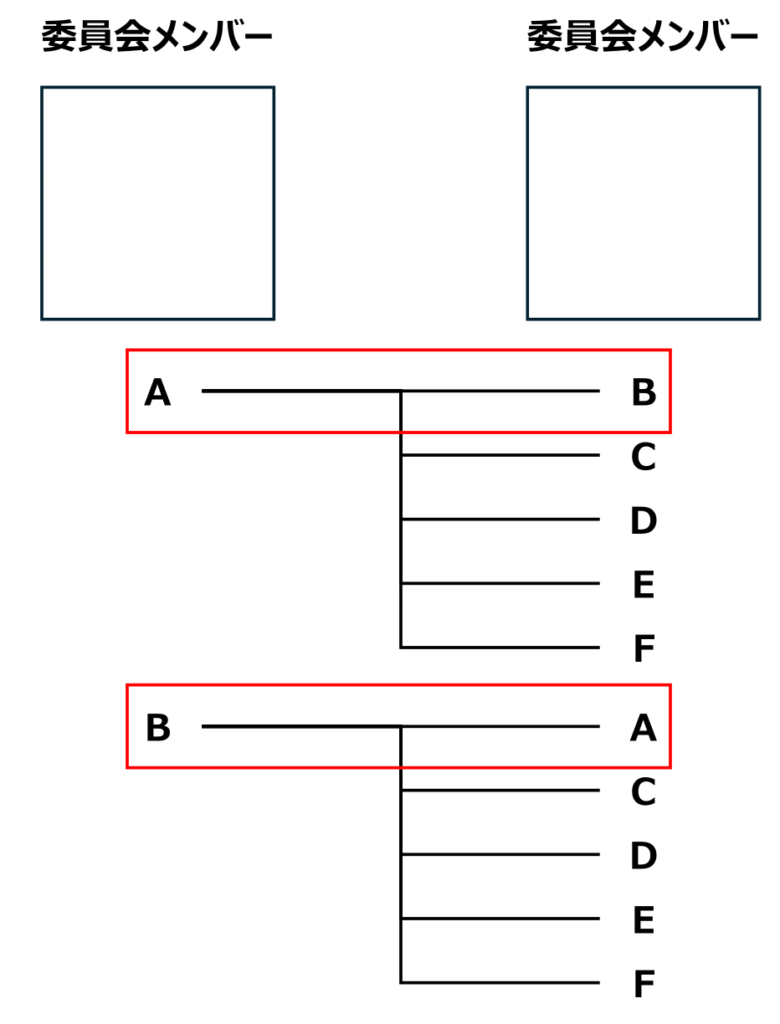
ならべ方を考えると、
6×5=30(通り)
ですが、上のように同じものを2つ数えてしまっているため、
30÷2=15(通り)
となります。
これを公式として、
★個の中から2個を選ぶときの選び方は
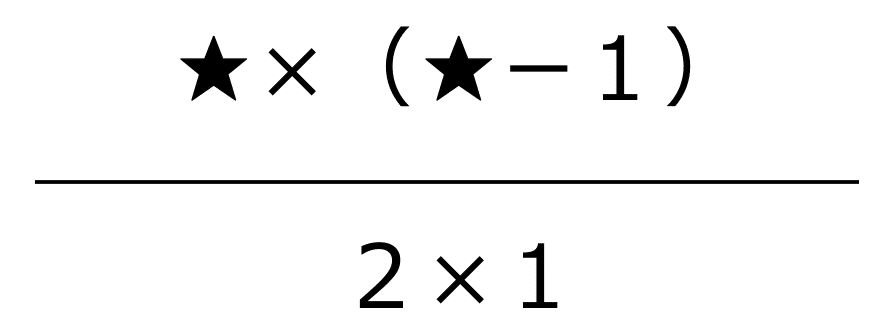
★個の中から3個以上を選ぶ場合も同じように、以下のようになります。

3人を選ぶ場合で考えてみると、以下のように同じ組み合わせを6個数えていることになってしまいますから、分母もかけ算を増やしていく必要がありますね。
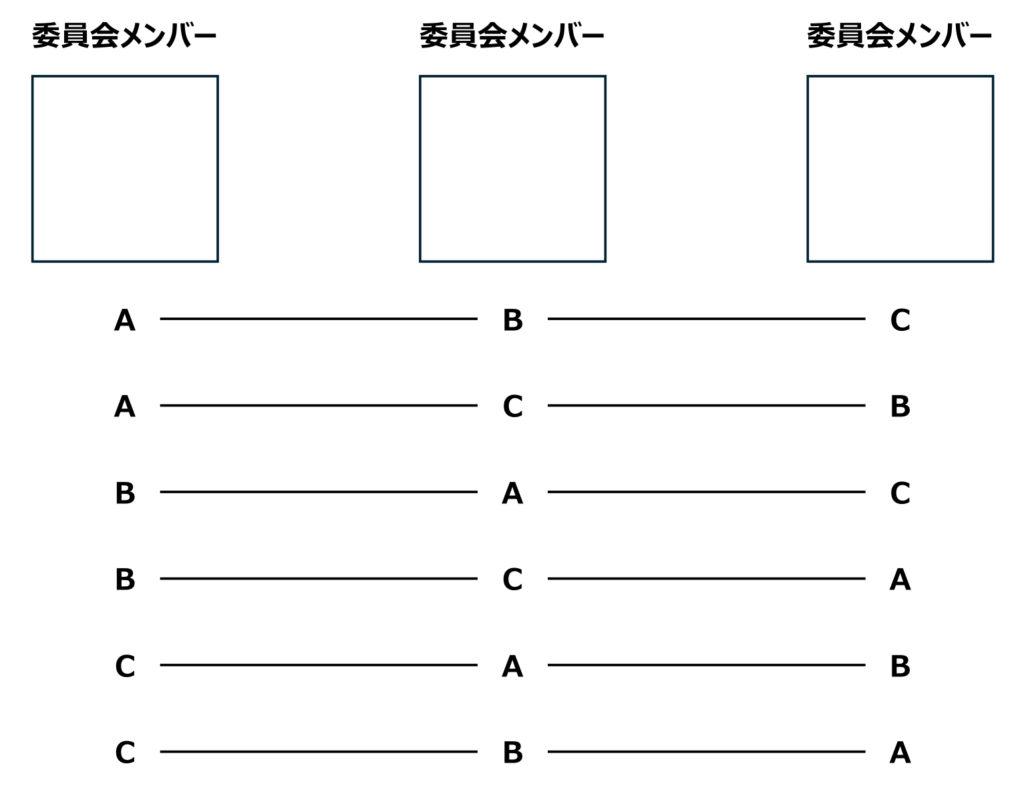
例題②:区別されていない複数の中から組み合わせを選ぶ
問題:赤いペンが4本、青いペンが3本、黄色いペンが1本あります。これらの8本の中から3本を選ぶとき、その3本の色の組み合わせは何通りありますか。
この問題では、置き場所も区別することができませんし、さらに、選ぶものも、赤いペン4本、白いペン3本を区別することができません。
さらに、この8本すべてを使うわけでもありません。
こういった場合は樹形図で丁寧に調べましょう。
必ず「赤⇒青⇒黄」の順で調べなければいけません。
例えば「青⇒赤」「黄⇒青」のように書き出してしまうと、すでに調べた組み合わせと重複してしまいます。
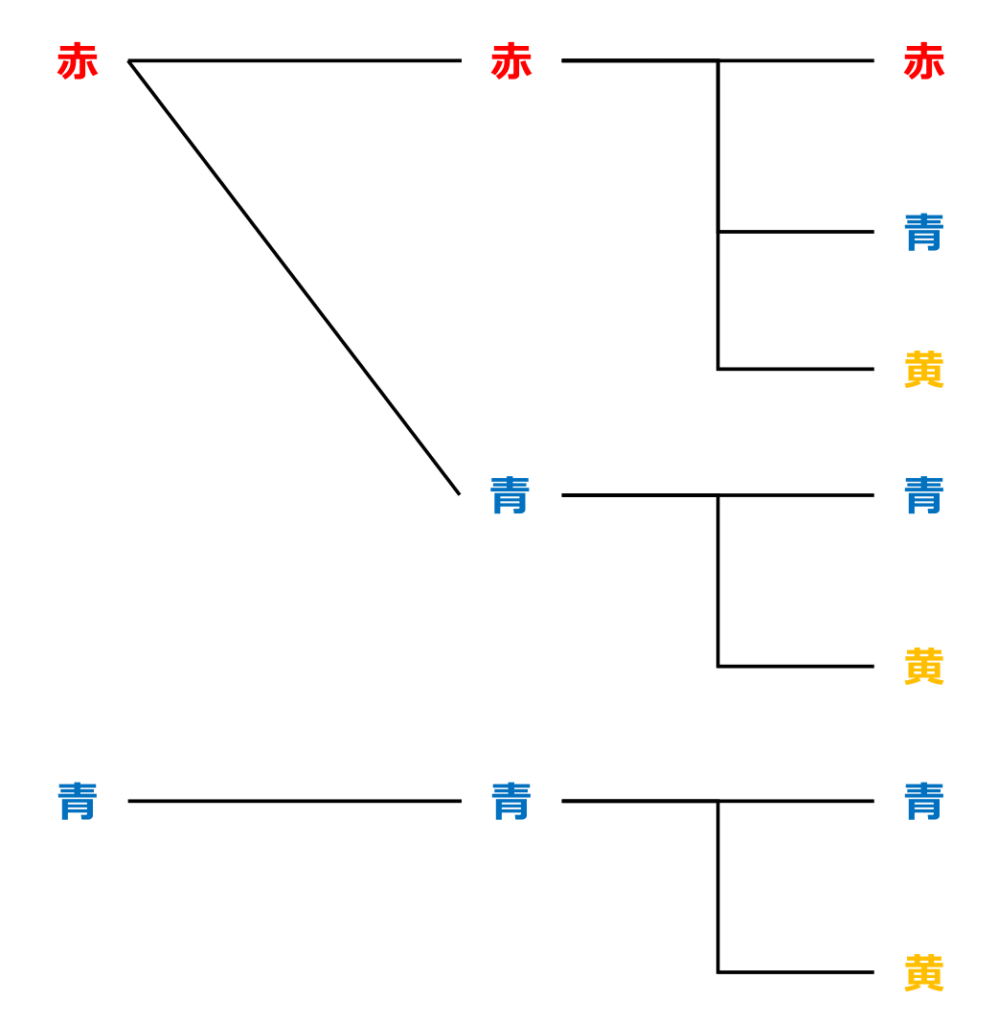
答えは7通りです。
例題③:区別できないものをならべる
問題:赤いボールが3個、青いボールが2個あります。これらの5個のボールをならべるとき、ならべ方は何通りありますか。
このような問題では、ならべ方の問題同様、まずは置き場所を考えます。
下の図のように、左から①~⑤の番号を振ります。
そして、この5か所のうち、どの2か所に青いボールを置くかを考えます。
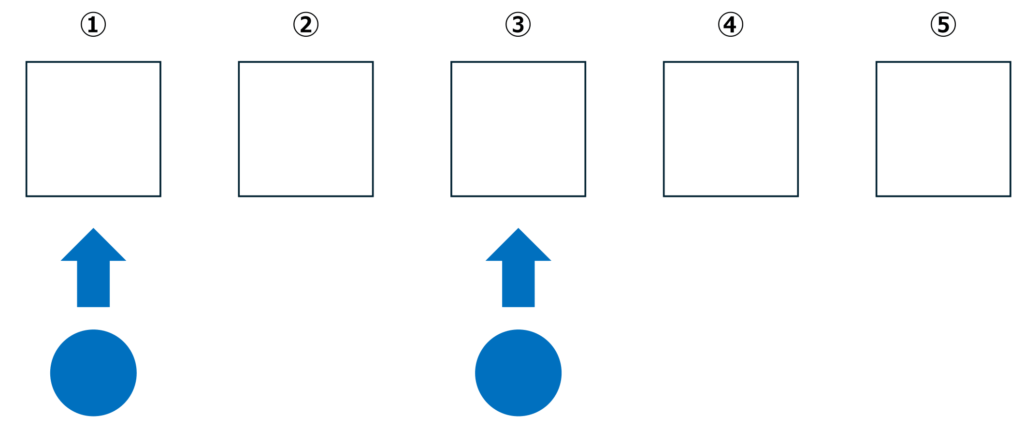
つまり、①、②、③、④、⑤の5か所の中から、青いボールを置く2か所を選ぶことになります。
これは例題①と同じ考え方です。
よって
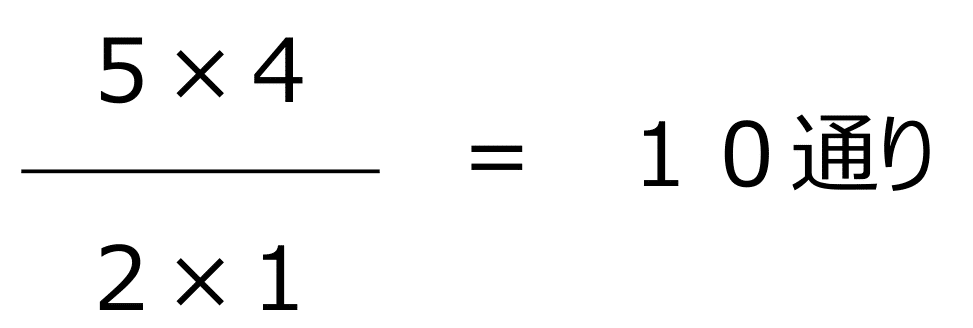
例題④:数に制限がないもしくは選ぶ数より多いものから組み合わせを考える
問題:赤いボールを10個、青いボールを10個、黒いボールを10個持っています。
この中から、5個のボールを選びます。全て同じ色でもOKです。5個のボールの選び方は何通りありますか?
5個のボールを選びますが、それぞれの色のボールは10こずつあり、5個のボールすべてが同じ色でも問題ありません。
このような場合は、5個のボールと、2つの仕切りを使って考えます。

2つの仕切りで3か所の空間にわけることができます。
一番左の空間にあるボールは赤色、真ん中にあるボールは青色、右にあるボールは黄色とします。
例えば以下のようなイメージです。
すべて同じ色でもよいことに注意しましょう。
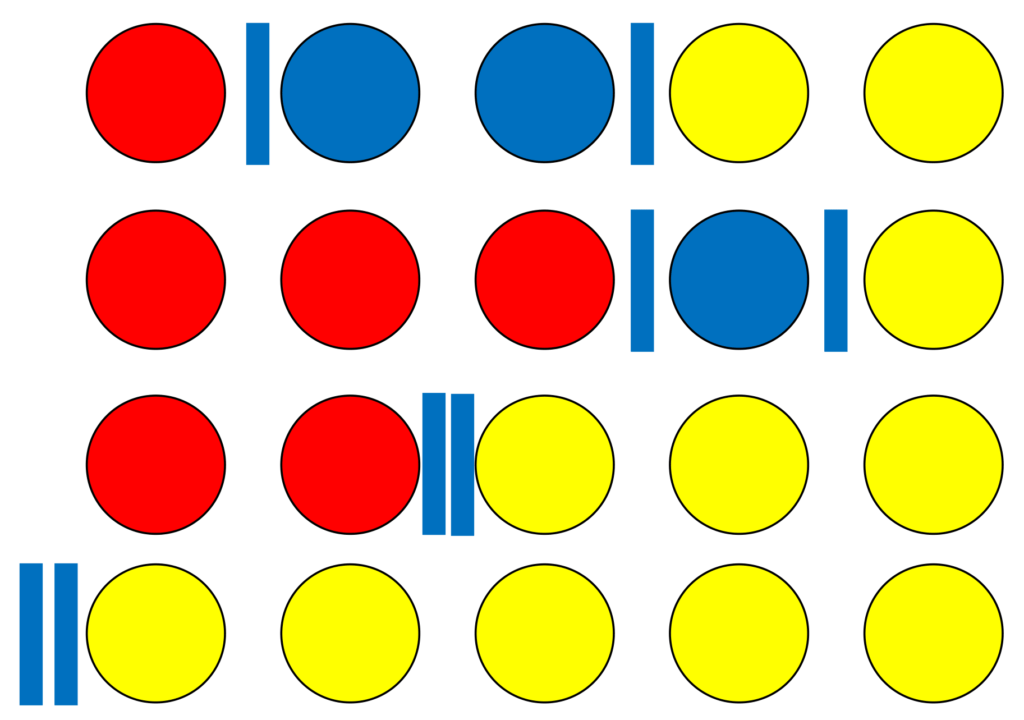
これにより、5つのボールと2つの仕切りのならべ方を考えれば、そのならべ方の結果に応じてボールが勝手に赤、青、黄色になってくれると考えます。
5つのボールと2つの仕切りのならべ方は例題②と同じく、7つの置き場所を考え、その中から、2つの仕切りの置き場所を考えます。(5つのボールの置き場所を考えてもOKです。同じ結果になります。)
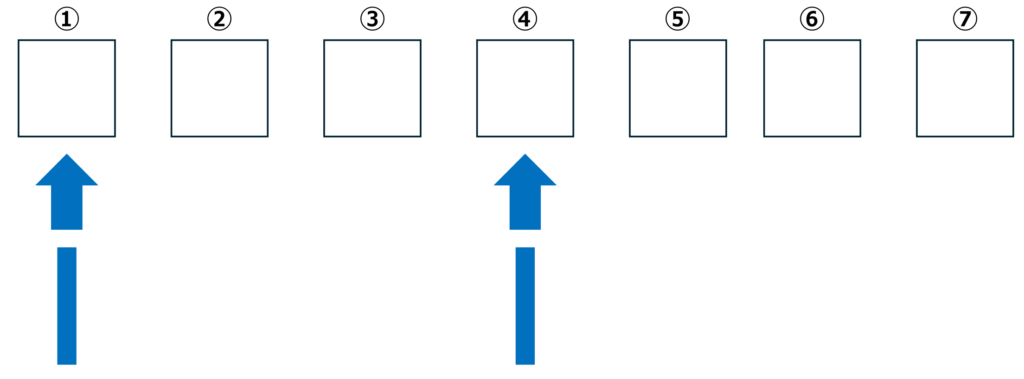
よって以下のように答えを求めることができます。
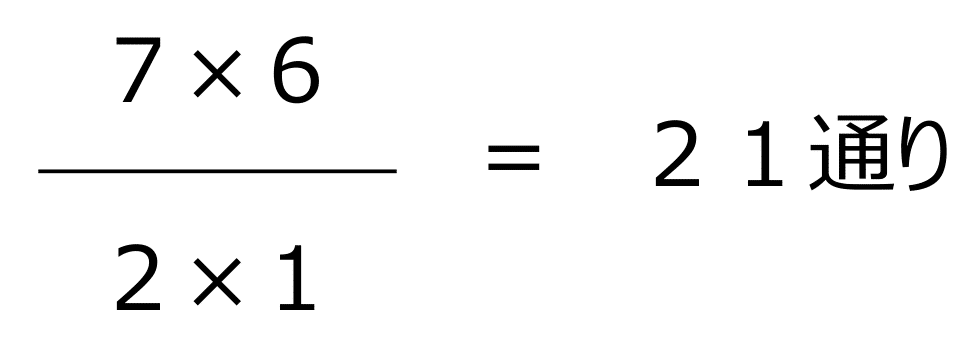
例題⑤:場合分けをして考える
問題:Aと書かれたカードが1枚、Bと書かれたカードが2枚、Cと書かれたカードが3枚、Dと書かれたカードが4枚、Eと書かれたカードが5枚あります。この10枚の中から5枚を選びます。選び方は何通りありますか。
この問題は例題②の問題とほぼ同じ問題です。
ただ、与えられたカードの種類、数、選ぶ枚数が多くなっています。
こういった場合は場合分けをして考えましょう。
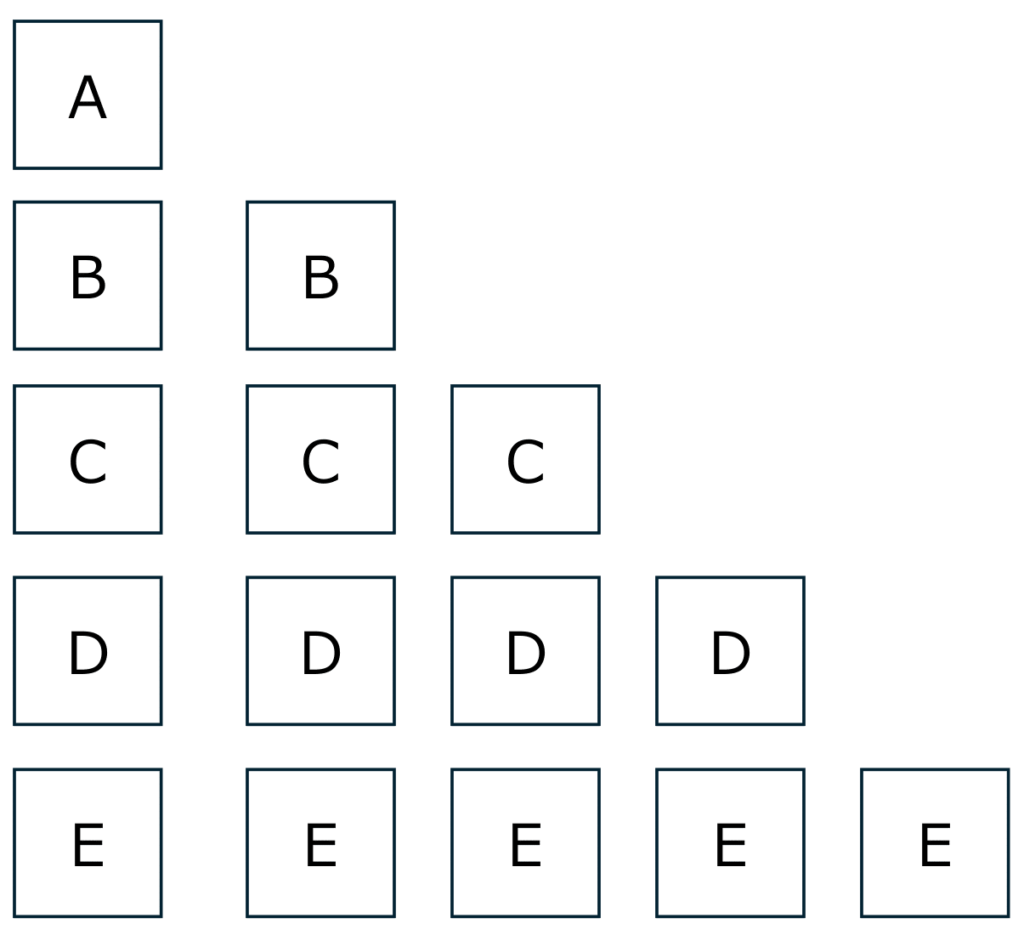
例題②と同様に書き出そうとすると、かなりのボリュームになってしまいます。
書き出しても問題ありませんが、慣れれば場合のわけのほうが早く、ミスを検証しやすくなります。
同じものをつかってもよい5枚の組み合わせとしては、
(5)
(4、1)
(3、2)
(3、1、1)
(2、2、1)
(2、1、1、1)
(1、1、1、1、1)
の7通りがあります。
★(5)=5枚すべて同じとき
すべてEの1通り。
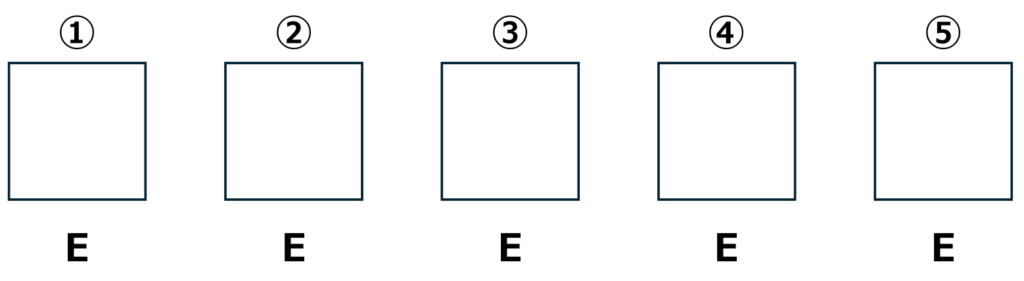
★(4、1)=4枚と1枚
同じ4枚のカードがD、Eそれぞれの場合がある。
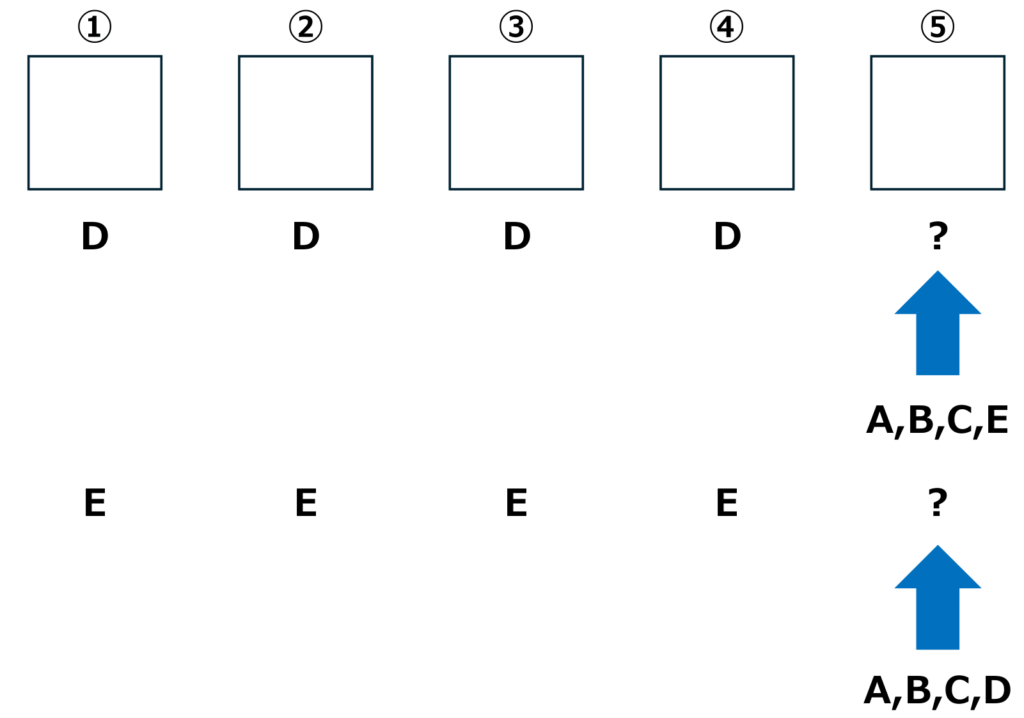
よって
4×2=8(通り)
★(3、2)=3枚と2枚
3枚のカードとして選ぶことができるのはC、D、Eの3種類です。
Cを3枚として選んだ場合、2枚の同じカードにはB、D、Eを選べます。
同じように、Dを3枚として選んだ場合はB、C、Eを、Eを3枚として選んだ場合はB、C、Dを選ぶことができます。
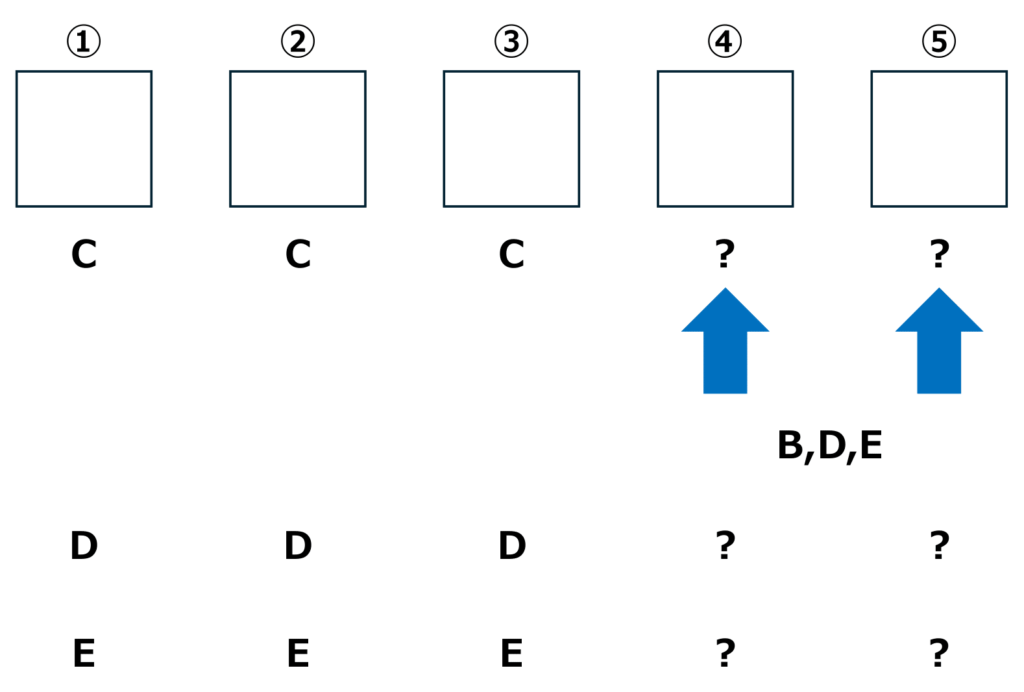
よって、
3×3=9(通り)
★(3、1、1)=3枚と異なる2枚
(3枚、1枚、1枚)の3種類のカードを使う場合です。
先ほどと同じように、同じ3枚のカードとして選ぶことができるのは、C、D、Eの3種類です。
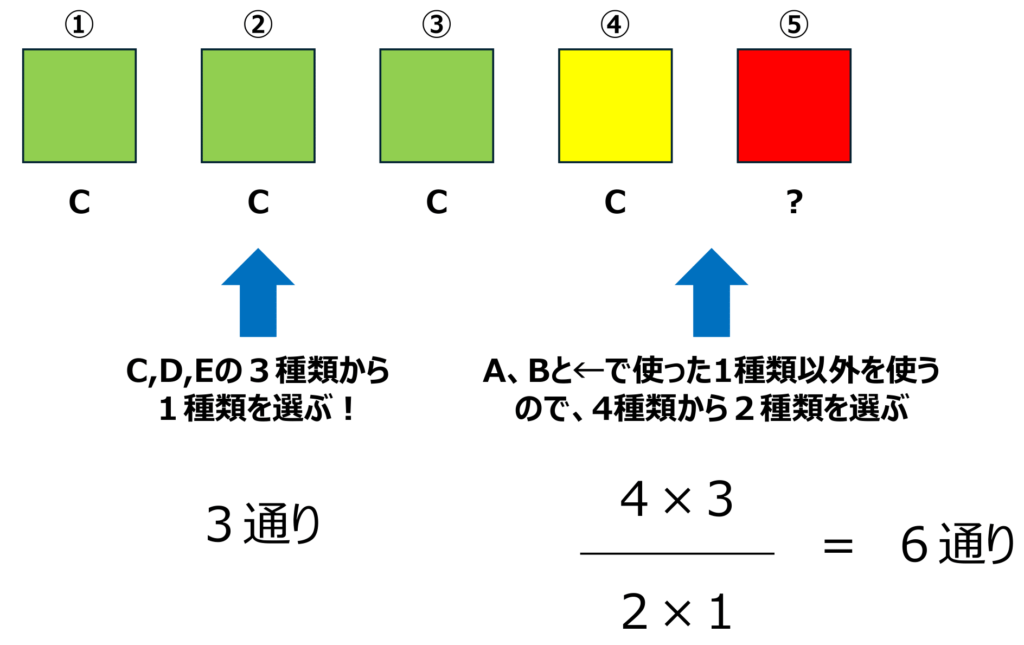
Cを3枚のカードとして選んだ場合、④、⑤には異なるカードを選ぶ必要があります。
ただし、④にB、⑤にDを選んだ場合と、④にD、⑤にBを選んだ場合では、組み合わせは同じになってしまいます。
つまり、A、B、D、Eの4種類から、④⑤に使う2種類を選びます。
3×6=18(通り)
と求められます。
■(2、2、1)=2枚ペアが2つと1枚
2枚使うカードはB、C、D、Eから2つ選びます。
残りの1枚には、A~Eの5種類の中からすでに選んだ2つを除いた3種類を使うことができます
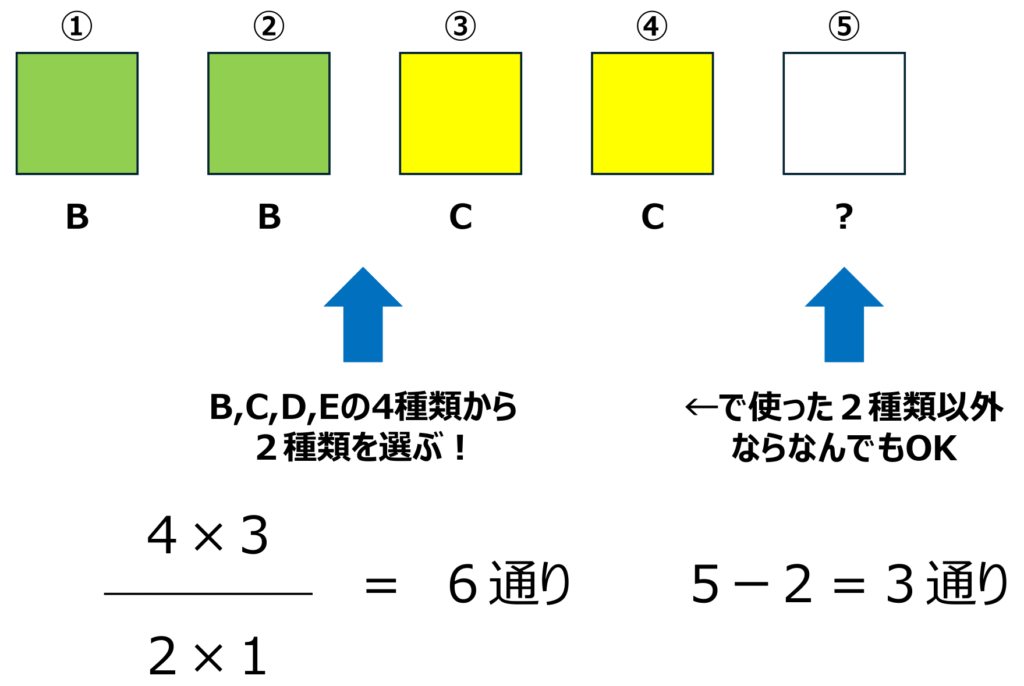
よって、
6×3=18(通り)
★(2、1,1,1)=2枚は同じで他はすべて異なる
2枚使うカードはB、C、D、Eの4種類から1つ選ぶので4通り。
残りの3枚は、残った4種類のうちから3つを選ぶ。
使わない1種類を選ぶのと同じなので、4通り。
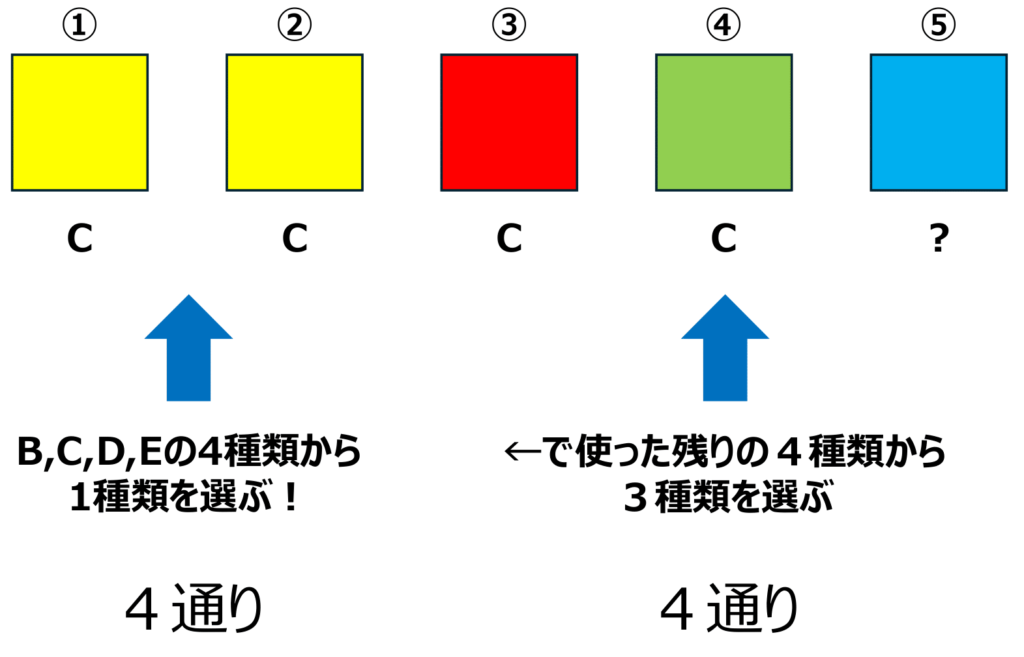
よって
4×4=16(通り)
★(1、1、1,1,1)=すべて異なるカード
A、B、C、D、Eをそれぞれ1枚ずつ使う1通りです。
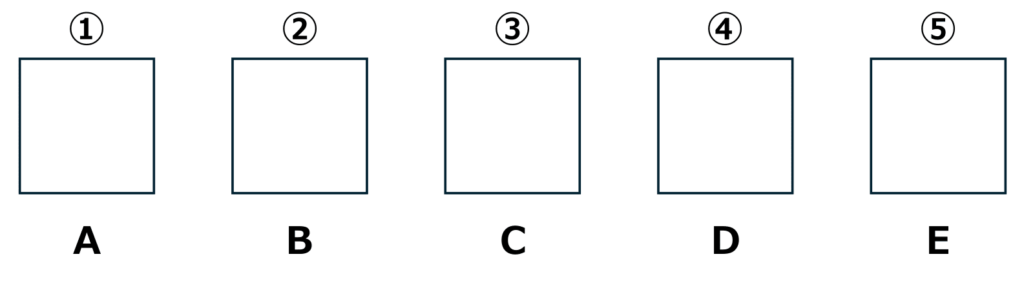
よって以上のすべての場合を足し合わせて、
1+8+9+18+18+16+1=71(通り)
問題:A、B、C、D、E、F、G君の7人が3人が泊まれる部屋「さくら」と5人が泊まれる部屋「うめ」に宿泊します。7人の泊まり方は何通りありますか。
「さくら」と「うめ」で合計8人宿泊可能です。
つまり、「さくら」に2人泊まる場合、「さくら」に3人泊まる場合で場合分けして考えます。
■「さくら」に2人、「うめ」に5人泊まる場合
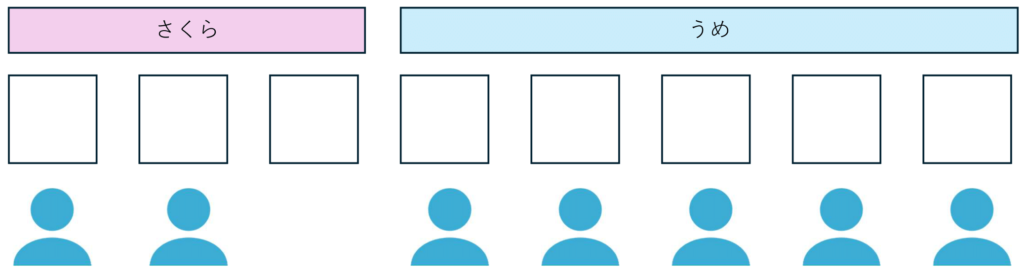
A~G君の中から、さくらに泊まる2人を選べば、残りの人はうめに泊まることになります。
よって
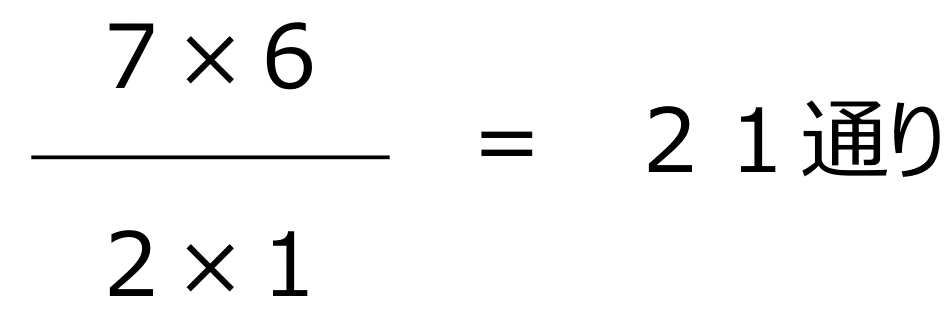
■「さくら」に3人、「うめ」に4人泊まる場合
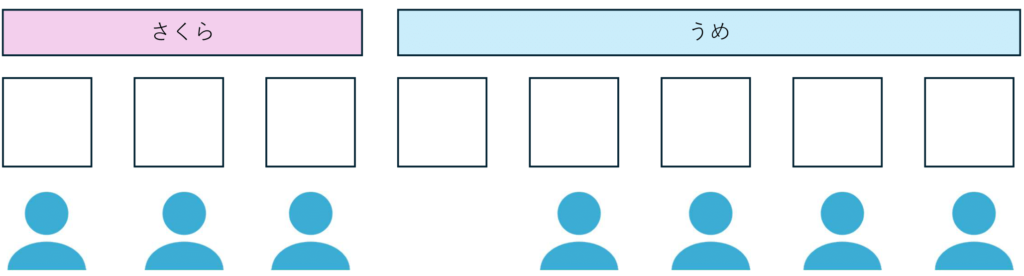
A~G君の中から、さくらに泊まる3人を選べば、残りの人はうめに泊まることになります。
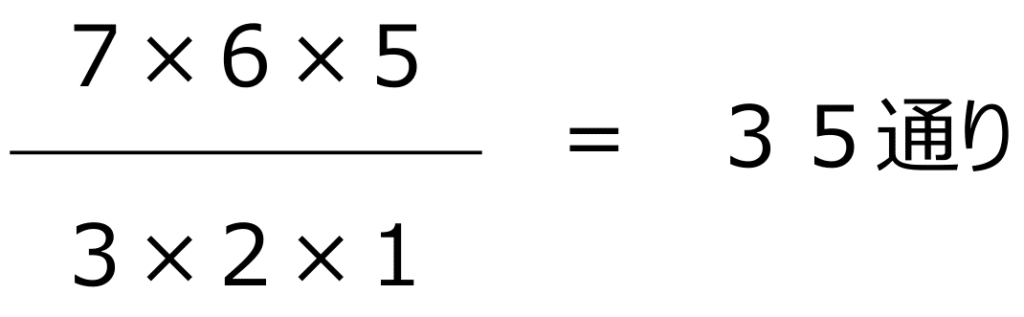
よって、
21+35=56(通り)
例題⑥:リーグとトーナメント
問題:A~Eの5人がじゃんけん大会を開催します。あいこで終わらず、必ず勝敗をつけるものとします。
(1)自分以外の全員とじゃんけんをする場合、全部で何試合行われますか。
(2)トーナメント形式で大会を開催する場合、優勝が決まるまでに何回じゃんけんが行われますか。
まず(1)の全員とじゃんけんをする場合を考えます。
リーグ戦(総当たり戦)と呼ばれます。
よく以下の表で表されます。
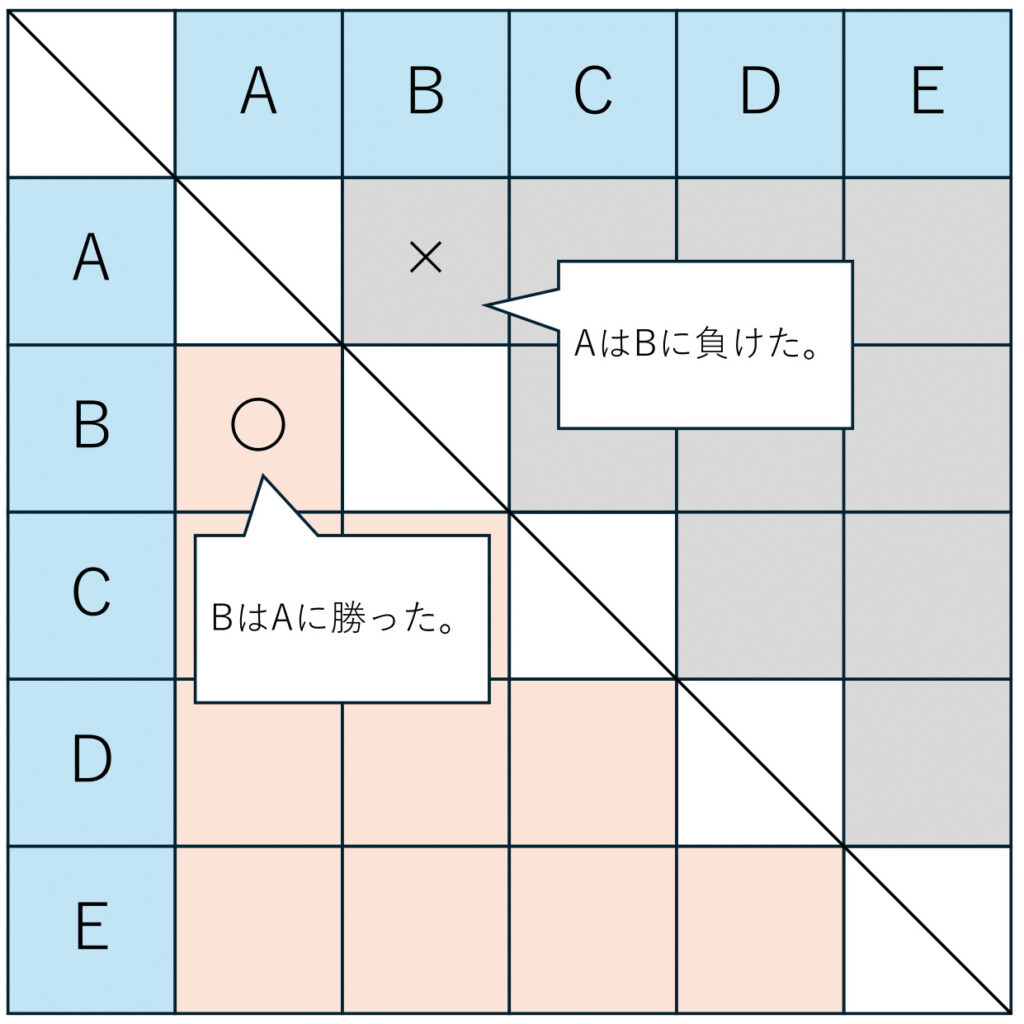
斜線を引いたマス以外は試合があることを意味していますが、「BはAに勝った。」「AはBに負けた。」というのは同じ試合のことを言っていますので、試合数の2倍のマスがあることになります。
マスは20個ですから、その半分の10試合が答えです。
また、A、B、C、D、Eが誰と対戦するかを樹形図で表すと下図のとおりです。
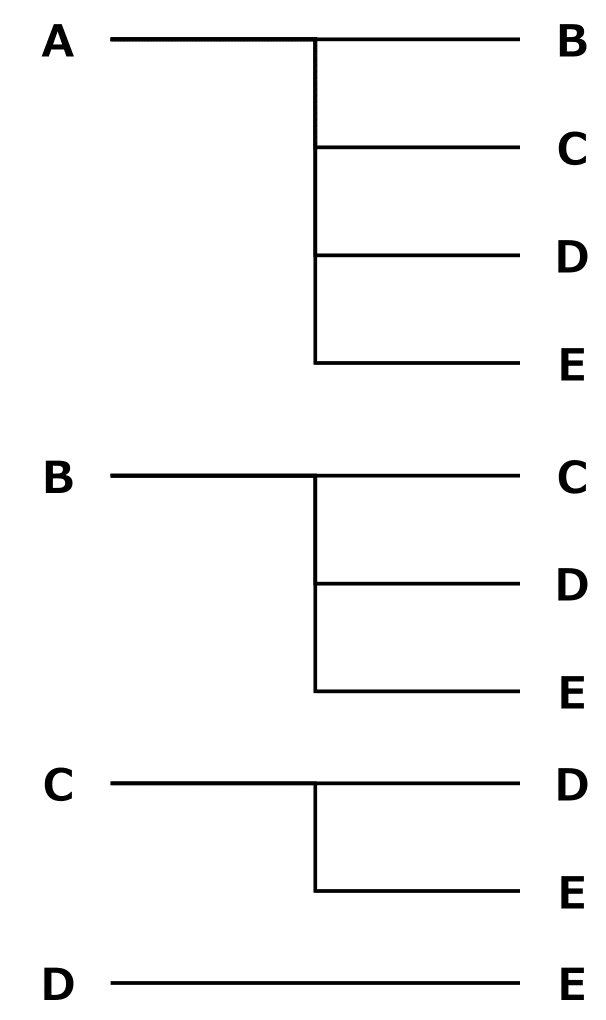
これでも10通りとわかります。
これらは、A、B、C、D、Eの5人から対戦する2人を選ぶと考えることができますので、
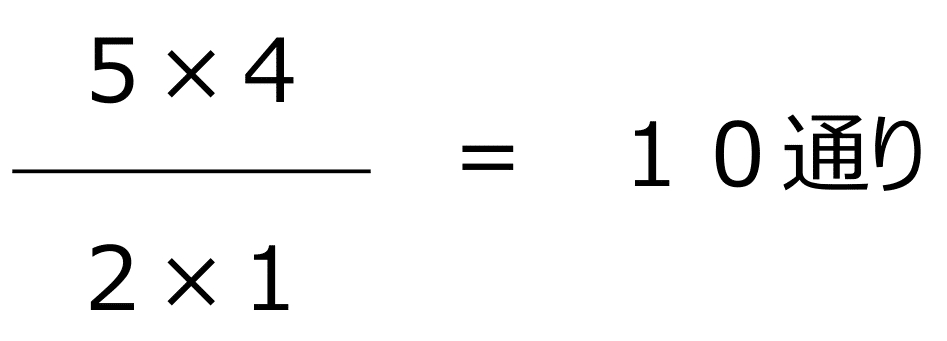
Nチームが参加するリーグ戦の試合数は以下の式で求めることができます。
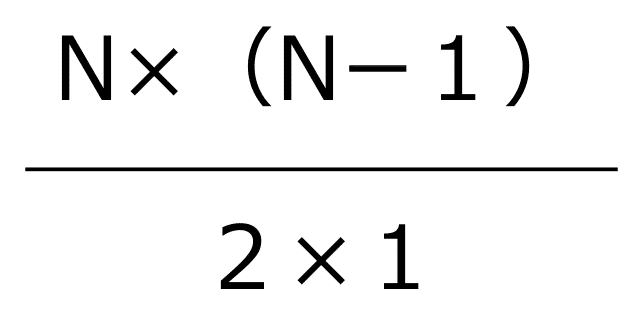
次に(2)のトーナメント戦を考えます。
トーナメント戦とは勝ち抜き戦のことです。
今回の5人でトーナメント戦をすると、以下のようになります。
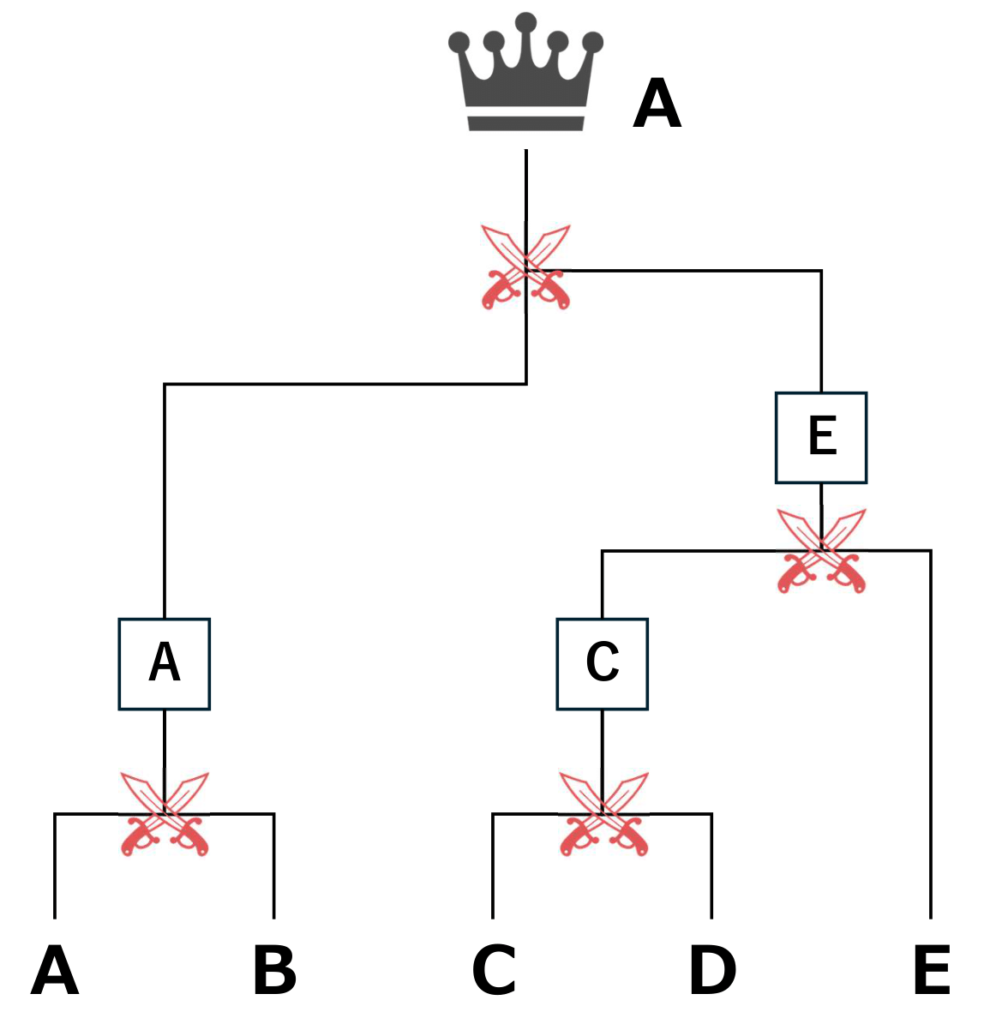
つまり、4試合行われます。
試合を「負けを1人(チーム)決めるもの」と考えてみましょう。
AとBのじゃんけんではBの負けが決まり、CとDのじゃんけんではDの負けが決まりました。
つまり、優勝を決めるまでトーナメント戦をする際に行われる試合数は、参加するチーム(人)の数から1(優勝者)を引いた数になります。
Nチームが参加するトーナメント戦の試合数は「Nー1(試合)」で求めることができます。
例題⑦:道順(ごばんの目)を組み合わせで考える
すでに扱った以下の問題を組み合わせで考えてみましょう。
問題:下の図のような道があります。A地点からB地点まで最短で行く進み方は何通りありますか。

A地点からB地点にたどり着くためには、必ず右に4回、上に3回移動しなければいけません。
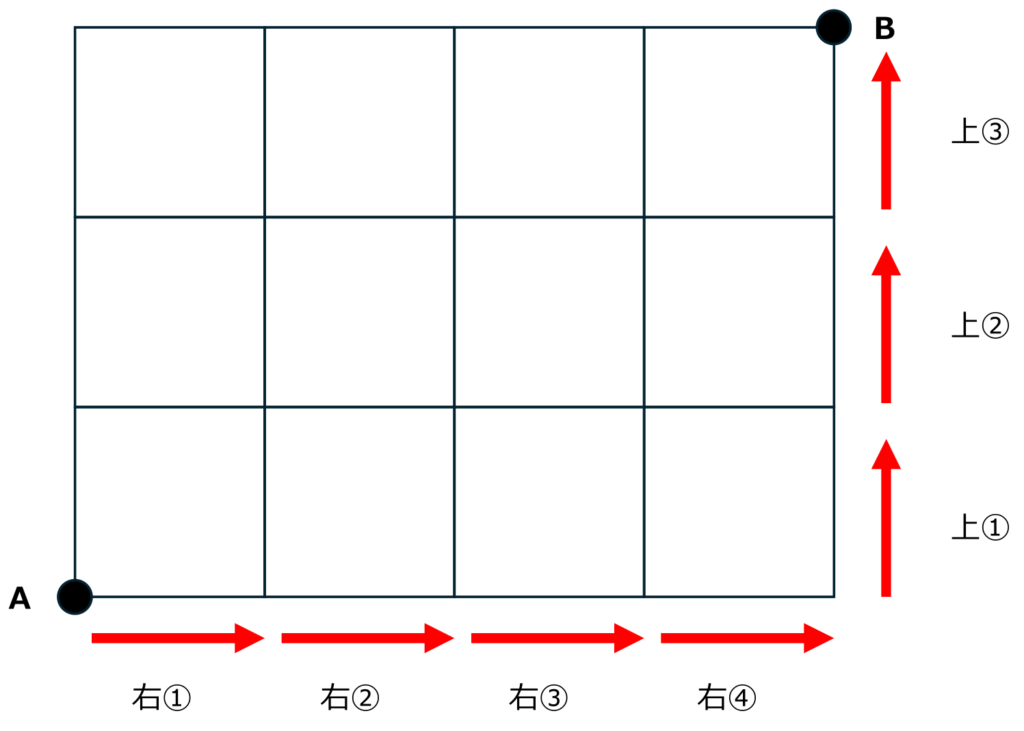
つまり、(右①、右②、右③、右④、上①、上②、上③)の7つのならべ方を考えればよいということになります。
以下のように2つの例を考えてみると納得がいくかもしれません。
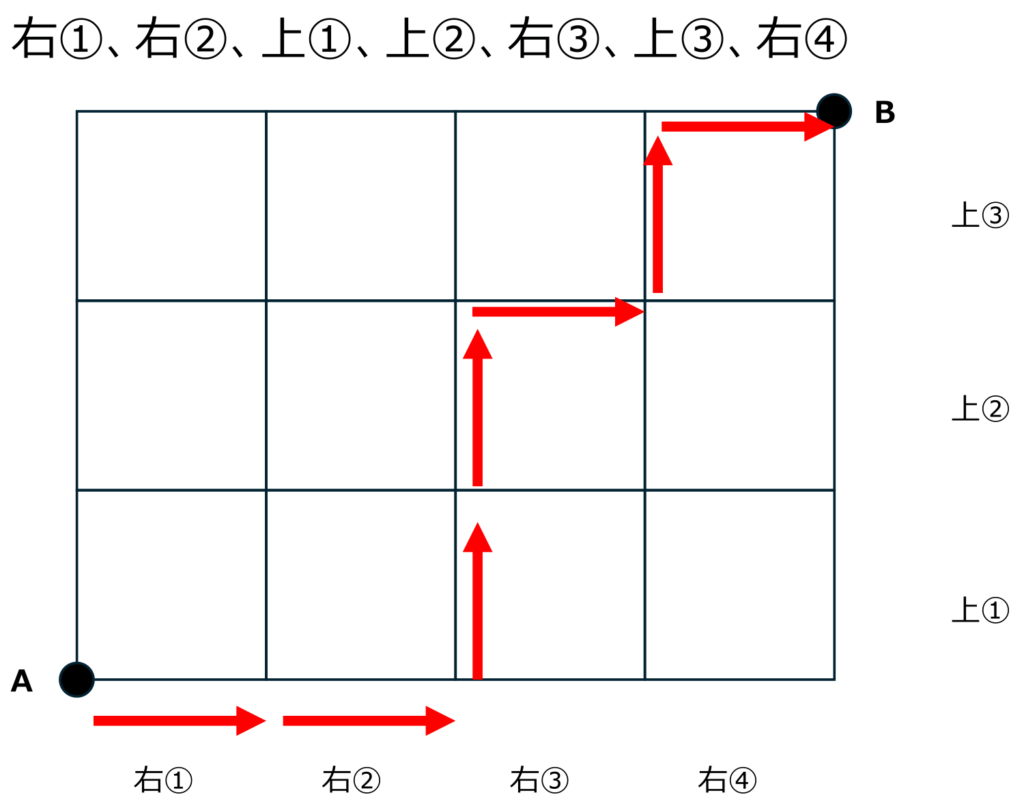
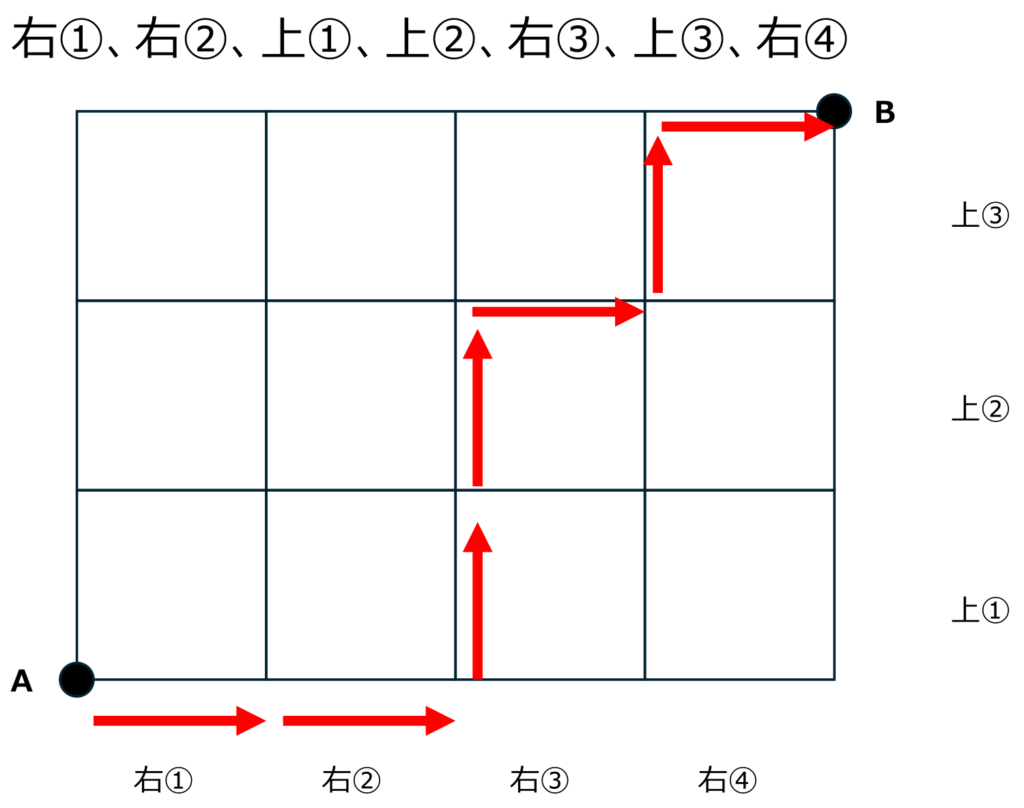
したがって、右①、右②、右③、右④、上①、上②、上③のならべ方を考えます。
ただし、右は必ず①、②、③、④の順にならぶ必要があり、上も①、②、③の順にならぶ必要があります。
右③、右①、右④、右②、左③、左②、左①
のようなならびだと、行き方として成立しないためです。
よって、7つの置き場所を考え、その中から、左①、左②、左③の置き場所を選べばよいということになります。
左①、②、③の場所を決めてしまえば、右①、②、③、④の場所は残りの4か所で決まり、左も右も左から順番に①、②・・・と番号は勝手に決まるためです。
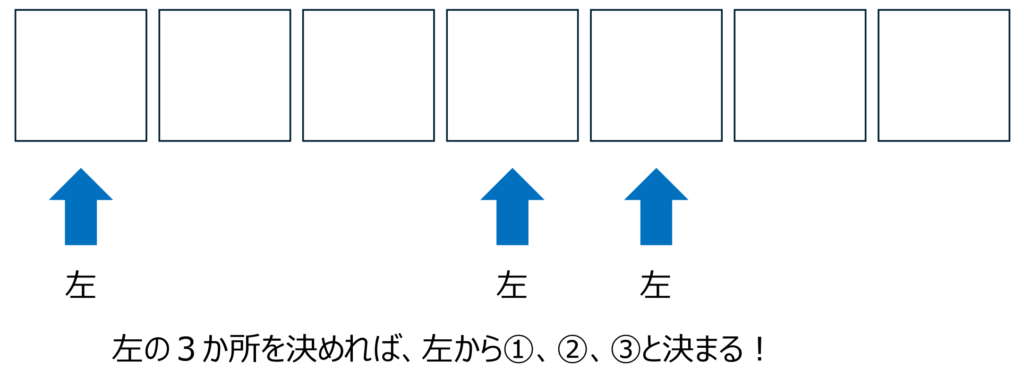
よって
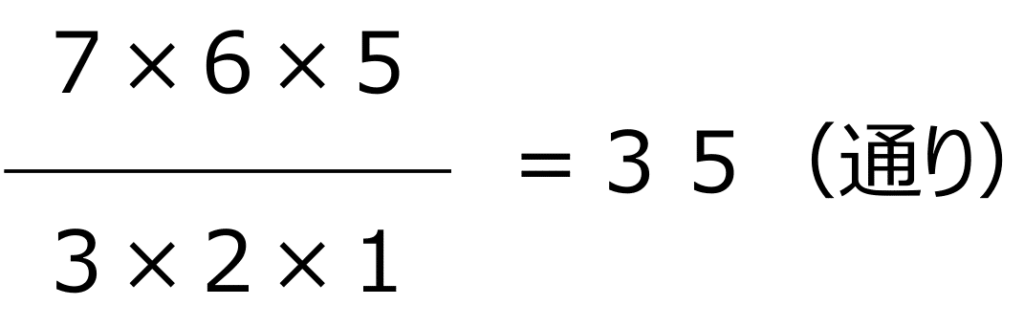
LEFYの中学受験個別指導
当塾LEFYでは、
- 集団塾の宿題がスムーズに進まない
- その結果、毎月のテストで思うような結果が出ない
- もっと勉強するように言うが、喧嘩になってしまう
- 今のレベルで第1志望は狙えるの?他にいい学校は?
- 計算ミスが減らない。図や式を書かない
などなど、中学受験を目指すご家庭の多くが抱えるお悩みに対して、お子さんの性格、タイプ、現在の学力に応じて、随時アドバイスしています。
一気に偏差値を10、20上げるような魔法はありません。
ご家庭、塾が協力しつつ、現状から少しずつでも改善し、勉強習慣を含めて基礎力をつけていくことで、最終的に6年生になったときに偏差値に結果が表れてきます。
堅実な成長を重ね、夢の第1志望校合格を狙いたい中学受験生はお問い合わせください。
中学受験のマンツーマン指導ならレフィーにご相談ください
レフィーの中学受験コースでは
- 社会人プロ講師
- 東大、早慶以上の大学生・大学院生講師(かつ難関私立中高一貫校卒)
※さらに、プロ講師、東大早慶以上の大学・大学院生の中からどちらも採用率20%程度
が完全1対1のマンツーマンで指導するため、着実に効果を感じられるはずです。
サピックス、グノーブル、四谷大塚、日能研、希学園といった集団塾と当塾レフィーを併用されている方、4科目すべてを当塾レフィーでご受講されている方がいます。
「とりあえず家庭教師・個別指導に通わせてるけど、あまり効果を感じられない…」
「集団塾の復習・理解が追い付かない!なんとか復習させないと…」
「中学受験は算数で決まるらしいけど、算数の成績が伸びない…」
とお悩みの方はぜひお気軽にご相談ください!
実際に効果を感じられ、志望校に合格されたご家庭がいます。
▼ぜひ見てみてください。
【2025年度】合格実績・合格者の声
▼お気軽にお問い合わせください!
(横浜駅徒歩7分。原則対面授業ですが、オンラインをご希望の方はご相談ください)
LEFY公式ラインでは、中学受験と中高一貫校生の勉強に関する情報を配信しています。
LEFYマガジンの記事を定期的に通知していますので、ぜひご登録ください!
